第四章 以太存在的证明

4.1. 在星系中存在的证明

星系的形状千姿百态，但星系总是遵守如下规律：

1. 星系的中心总是有一个大质量的黑洞；
2. 星系的可见物质质量总与黑洞的质量成正比；

   3. 星系外围恒星的旋转速度总是趋于一个常数，如图4-1所示。

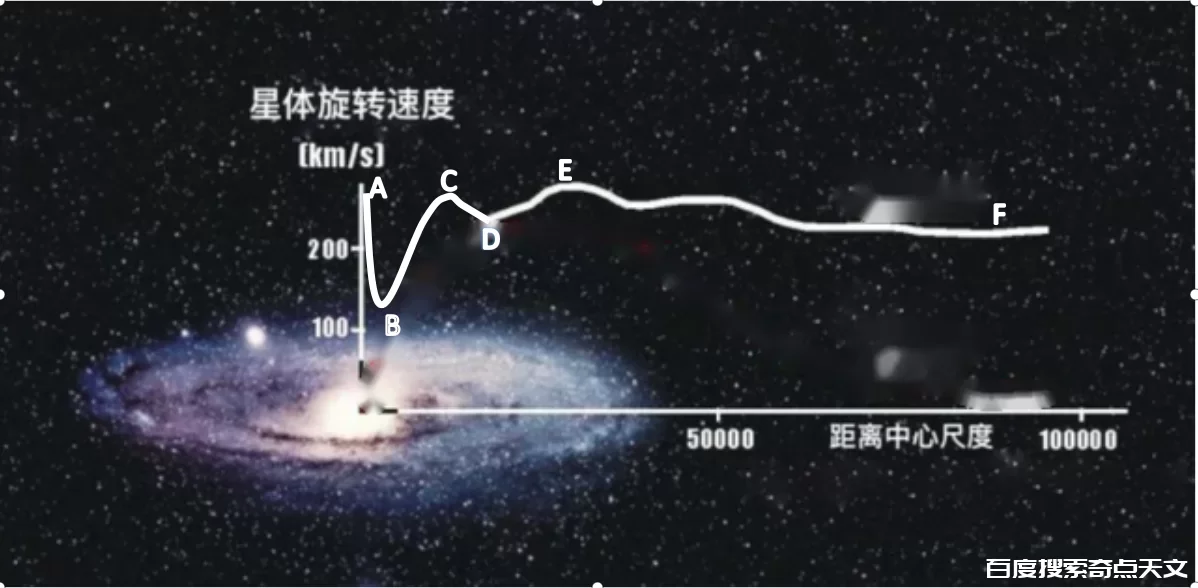
                             图4-1.星系中恒星的速度分布曲线

星系外围恒星的旋转速度一直使天文学家百思不得其解，不得不引入“暗物质”来解释它，但暗物质在哪里？

4.1.1. 以太是如何产生引力的

   如果引入以太，就很容易解释这种现象。

   由于以太是流体，在大质量物体附近的密度总是比远处的高，物体的质量越大，以太的密度就越高，在星系中以太的密度分布如图4-2所示。

                     图4-2.星系中以太的密度分布示意图

以太也是具有质量的物质，当然能产生引力，但它与普通物质产生引力的方式不同，如果以太的密度处处相同，当然没有引力质量可言，就象在空气中称量空气，是称不到重量的，但如果密度不同，以太就能够表现出引力质量，就象在空气中称量压缩空气一样，是能够测量出空气质量的。

以太的引力质量与它的密度差有关，密度差越大，所表现出来的引力质量就越大。如图4-2所示，假设在星系中心处有一块体积为V的以太，如果观察者在中心观察，这个体积为V的以太所产生的引力质量为0，但随着观察者向外围移动，就会观察到这个体积为V的以太，其引力质量越来越大，而且可以超过可见物质的引力。

举个例子，在银河系，以太的平均密度为1.257×10^-6 kg/m³，可以计算出每立方光年的以太，其绝对质量为1.06×10⁴² kg，比整个银河系的可见物质还重。如果以太在银河系中的分布是均匀的，所表现出来的引力就是各向同性的，也就无法显示以太的存在。假设太阳系中以太的平均密度为1.25700×10^-6 kg/m³，银河系中心10光年内以太的平均密度为1.25701×10^-6 kg/m³，则从太阳系看，以银河系中心，半径10光年内以太的引力质量为3.54×10⁴⁰ kg（计算方法是：以太的体积与两地密度差的积），是太阳质量的一百多亿倍，如果在银河系的外部看，这部分以太将具有更大的引力质量。由于以太看不见，科学界又不承认以太的存在，也就成为了天文学家所说的“暗物质”。可以看出：以太的引力质量并不是不变的，在不同的区域，所表现出来的引力质量并不相同，离中心越远的地方观察，中心区域的以太所表现出来的引力质量就越大。

4.1.2. 恒星速度分布曲线的解释

现在可以解释图4-1中的恒星速度分布曲线了，这个速度曲线可分为三个部分：从A到B，是星系的核心部分，恒星的速度主要由中心黑洞的质量引起的，以太所起的作用很小，可以忽略不计，与太阳系中的行星运动具有相同的规律，符合开普勒三大运动定律。从B到C，以太的引力开始起主要作用，由于星系的核心呈球型，以太的引力质量与半径正相关，而且以太的引力质量的增长速度比半径增加的快，从而导致恒星的速度也随着半径的增加而增大。例如，在银河系，引力质量与半径的关系可表示为：M_d=2.61×10¹⁶r^1.24。从C到F，随着星系半径的增加，由于星系的结构变为园盘形，引力质量与半径的关系变为近似线性，恒星的速度也变为近似常数，在D点，恒星的速度有一定的下降，是由旋臂引起的（旋臂中的以太密度高，如果星系中没有旋臂，恒星的速度曲线变化就不大）。

正是由于以太参与引力的作用，才保证了银河系中心对外部星体的强大引力，以太是维系星系外围旋转速度的关键物质。

4.1.3. 引力透镜现象

引力透镜效应是爱因斯坦的广义相对论所预言的一种现象，如果在观测者到光源的直线上有一个大质量的天体，则观测者会看到由于光线弯曲而形成的一个或多个像，这种现象称之为引力透镜现象。相对论的解释是：由于时空在大质量天体附近会发生畸变，使得光线经过大质量天体附近时发生弯曲，但弯曲的时空很多人都无法理解。

从图4-2可以看出：以太的密度分布很像一个凸透镜，如果光线通过一个星系时，根据凸透镜的原理，引力透镜现象就很容易让人理解，因为以太是光的传播介质，而光线会向着介质密度大的方向折射。

4.2. 在太阳系中的存在证明

由于以太在太阳系中的密度变化很小，所产生的引力质量可以忽略不计，因此，在太阳系中观察不到“暗物质”的存在，但以太的运动所产生的效应却是非常明显的，主要表现有二：

A. 引力拖动效应

大质量星体附近的以太跟随星体一起运动的现象称为引力拖动效应，这种效应表现最明显的是海王星上的巨大风暴，海王星上的风暴是由于海卫一逆行间接产生的，其直接的原因是海卫一拖动以太，再由运动的以太与海王星大气进行动量交换而产生的。类似的情况在太阳系中相当普遍，例如，太阳的较差自转就是水星间接产生的。如果没有以太，海王星上就不会有巨大的风暴和太阳系中最明显的较差自转（其赤道自转周期约为18小时，两极约为12小时）。

B. 以太的涡旋运动

太阳系中八大行星的运动，在太阳系中产生了众多的以太旋涡，最明显的就是金星上的大气环流，金星附近的以太气体在地球和水星引力的拖动下，在金星周围形成了以太涡旋一直绕金星旋转，造成了独特的金星大气环流，进而导致了金星的逆向自转，没有以太的作用，金星上的大气环流是无法解释的。另外，每个行星外围的逆行轨道也是以太涡旋存在的最好证明。

4.3. 在地球上的存在证明

在地球附近，以太的密度基本各向同性，更观察不到暗物质存在的现象。在大气层内，以太相对地球表面也没有明显的运动，也观察不到以太的运动现象。以太是中性流体，也不参与电磁作用，其唯一的作用就是光的媒介，没有以太就没有光（电磁波）。在地球上，空气对于声音，与以太对于光，其作用基本相同，下面通过比较以太与空气中波的传播特征来证明以太的存在。

4.3.1. 光速与声速的比较

很多的实验都可以证明：光速不变而且与发射体的运动状态无关，但所有的实验都有一个前提，就是观察者相对于传播介质是静止的，也就是说，只有观察者相对于传播介质是静止时，光速才是不变的。声音也有同样的性质：当观察者相对于空气静止时，声音的传播速度也同样与发射体的运动状态无关，只要空气的温度不变，声音的速度就是确定的，这是经过很多实验证明过的，与光速的性质完全一样。

如果观察者相对于介质是运动的，所观察到的速度就是可变的，例如：一列长度为L的敝蓬列车，在列车的首尾各有一人A和B（A在前），当列车以速度V前进时，如果A呼叫B，则B听到A的声音所需要的时间为：t₁=L/(V+C)，如果B呼叫A，则A听到B的声音所需要的时间为：t₂=L/(C-V)，其中，c为声音在空气中的传播速度，也就是说，观察者A所观察到的声音速度是C-V，而B观察到的声音速度是C+V，但如果观察者在地面，所观察到的声音速度都是c，而不管列车处于何处，也不管列车的速度是多少，对于观察者来说，相对于传播介质是否运动才是波速是否变化的根源。

著名的萨格纳克效应就是一个观察者相对于介质运动的例子。这个实验与上述敝蓬列车具有相同的原理，在这个实验中，光源与屏幕（观察者）之间的距离不变，两条光路的距离一样，当这个平台旋转时，两条光路的速度不一样（相对于观察者），从而导致两束光到达屏幕的时间不同，使干涉条纹发生移动。这个实验证明了三点：一是干涉条纹移动数与干涉仪的角速度和环路所围面积成正比，二是光的传播需要介质，三是光相对于介质的传播速度是恒定的。如果光的传播没有介质，萨格纳克效应是无法解释的。中日双向时间传递实验证明了地球自转具有萨格纳克效应，也证明了地球大气层以外的以太是相对地球表面是运动的（地球表面的以太相对地球静止）。对于观察者来说，光源相对介质的移动和观察者相对介质的移动不是等价的。

如果光的传播不依靠介质，是解释不了光子是如何发射的、如何达到光速的，也无法解释光通过透明物体后光的速度是如何重新变快的。光既然是波，它就和所有的波一样，是一种介质的波动。例如：在空气介质中的声音，尽管声源振动的频率有快有慢、振幅有大有小，但声音的速度却是恒定的，因为介质都有自己的内在固有属性，除非温度变化了，音速才会改变。同理，光也是波，传播同样需要介质，传播速度取决于介质，而与光源无关，不管波动频率和初始能量多大，只要介质的性质不发生变化，光速就是恒定的。如果没有介质，光在传播过程中没有任何速度恒定机制存在，而光的发射源和发射过程也没有任何速度恒定机制，因此，没有介质的光速是不可能恒定的。

可以得出结论：光速不变的原因，一是由于它是在以太中传播的波，传播速度取决于以太的温度；二是观察者相对于以太必须是静止的，如果观察者相对以太不是静止的，观察者所观察到的光速也会发生变化。在宇宙中，光速的值并不是恒定的。与音速一样，光速的大小也依赖于介质的温度。例如，声速与空气温度的关系可表示为：，光速与以太温度的关系可表示为：。只有介质的温度不变时，光速才是恒定的，高密度星体附近的以太温度高，光速值大。

4.3.2. 多普勒效应的比较

多普勒效应是当波源与观测点之间存在相对运动时，观测点实际接收到的频率并不等于波源实际频率的现象。

A. 声波的多普勒效应

声波为什么具有多普勒效应呢？声波之所以会产生多普勒效应，是由于声波传播具有如下三个特征决定的：

     1.声源与声波之间存在速度的叠加

声源与声波速度的叠加指的是：产生声音的物体，其相对于介质的运动速度与振动速度的叠加，当声源相对于传播介质的运动速度为零时，声波与声源之间的相对速度等于音速，当声源相对于传播介质的运动速度不为零时，声源的运动速度与振动速度的叠加可使一个周期时间内的波长长度发生变化，这种波长的长度变化量等于声源相对介质的运动速度乘以声波的周期。与波源运动同向传播的波，其波长是变短的，与声源运动反向传播的波，其波长是变长的。

     2.声波的传播速度只与介质的物理性质有关，而与声源的运动状态无关。

在一定的物理条件下，无论声源的运动状态如何，声波的传播速度是不变的。声速之所以与声源的运动状态无关，是因为声波只是能量传递的一种形式，一旦声波离开声源，声源的运动对声波不再起任何作用，声波将依据介质的传播特点进行传播。

     3.接收者与声波之间也存在速度的叠加

声波的产生和接收过程相似，接收是产生的逆过程，在接收的过程中，如果接收者相对于传播介质的运动速度不为零，接收者的运动速度与波动速度的叠加，也可使一个周期时间内的波长长度发生变化，这种波长的长度变化量等于接收者相对介质的运动速度乘以声波的周期。与接收者运动同向传播的波，其波长是变长的，与接收者运动反向传播的波，其波长是变短的。当波源静止，而观察者以速度v靠近波源时，由于波源静止，介质中声波的频率与波源频率相等。根据接收频率的定义（1s内连续通过接收者的完整波的个数），可以得出：1s内波传播了s₁=ux1，同时观察者在1s内向前移动了s₂=vx1。所以波在1s内相对于观察者的传播距离就是这两段距离之和，因此，接收者所接收到的频率：，如图4-3所示。

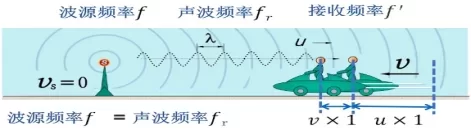
            图4-3.波源静止时的多普勒效应（图片来源于乞力马扎罗山的雪B）

当波源相对于介质向右运动时，波源在运动过程中向四周发出声波，等相位面就变成了一系列偏心圆环，沿着波源的运动方向，波长发生了压缩，如图4-4所示。

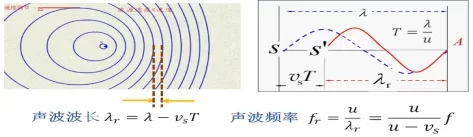
           图4-4.波源运动时的多普勒效应（图片来源于乞力马扎罗山的雪B）
如果波源静止，S点发出的波经过一个周期以后传播到A点，S点与A点之间的距离就是此时的波长λ。由于波源是运动的，当波传输到A点的时候，波源从S点运动到了S’点，它们之间的距离就等于波源的移动速度vs乘以运动周期T，根据波长的定义，S’点与A点之间的距离就是此时的波长：，介质中声波的频率为。如果接收者相对介质是静止的，所接收到的频率与介质中的频率相同，如果接收者相对于介质以速度v向着波源运动，则所接收的频率为，如果接收者相对介质与波源运动的运动方向相同，则所接收的频率为，当接收者与波源的相对速度为0，则不论波源相对介质的速度是多少，所接收的频率总是与波源相等。

需要指出的是：波源相对介质的运动与接收者相对介质的运动不是等价的，例如，假设波源的频率为f，当波源相对介质以0.5u的速度向接收者运动时，接收者相对介质静止时所接收到的频率为2f，但当波源相对介质静止，而接收者以0.5u的速度向波源运动时所接收到的频率为1.5f。

B. 光波的多普勒效应

学界主流认为，光波中的多普勒效应是相对论效应，是通过相对论的时空变换方程计算出光波频率的变化量：，其中，v是波源与接收者的相对速度（当相互靠近时v取正值，否则取负值）。在相对论中，假设光速不变，而且是相对任何惯性参考系都不变的物理量，这种假设已经超出了人们对速度概念的认知。依照光速不变性原理和相对性原理，如果波源的频率不变，而光波的速度又与光源的是否运动无关，因此，光的波长是不可能变化的，多普勒效应也就失去了存在的理论基础。光速不变是可以理解的，因为声速也是不变的，但速度是必须存在参考系的，声速不变指的就是相对于介质，没有参考系就没有速度。萨格纳克效应已经证明：当观察者相对介质运动时，光速是可变的，波源与观察者的运动并不等价。因此，相对论也就失去它的理论基础，通过时空变换方程推导出的光波频率变化量也必然是错误的。

但是，要想证明这是一个错误是非常困难的，例如：频率为10 GHz的波源以1000 m/s的速度运动时，计算所接收到的频率差，如果以声波中的多普勒公式所计算的结果是：= 33356.52 Hz，如果以光波中的多普勒公式所计算的结果是：= 33356.47 Hz，前面的5位数都是一样的，现代的技术水平还不能分辨出谁对谁错。随着技术的发展，真相总有大白的时候，相信光波的多普勒效应的原理与声波完全一样，计算方法也应该是完全一样的。

任何物理现象，必然存在物理过程。在声波中，多普勒效应产生的物理过程非常清晰，而在光波中，只存在坐标系的变换和数学上的推导，却没有物理过程的说明。声源相对于声波可以有相对速度的叠加和变化，这种相对速度的叠加和变化才是多普勒现象产生的原因，而相对性原理和光速不变原理根本不容许光源与光波有相对速度的叠加和变化，既然没有相对速度的叠加和变化，那么类似于声波传播中发生的多普勒效应又如何在光波传播中发生呢?光波波长又如何变化呢？

4.3.3.萨格纳克效应比较

萨格纳克效应是指1913年萨格纳克发明的一种可以旋转的环形干涉仪。将同一光源发出的一束光分解为两束，让它们在同一个环路内沿相反方向循行一周后会合，然后在屏幕上产生干涉，当在环路平面内有旋转角速度时，屏幕上的干涉条纹将会发生移动，如图4-5所示，这就是萨格纳克效应，萨格纳克效应中条纹移动数与干涉仪的角速度和环路所围面积成正比。

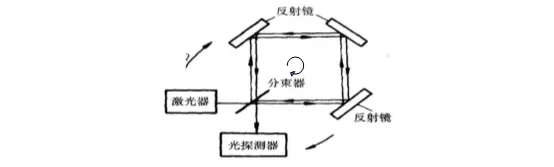
                                       图4-5.萨格纳克环形干涉仪

萨格纳克效应产生的原因是介质的相对运动，是光源和观察者相对静止，介质运动所产生的现象。与多普勒效应恰好相反，多普勒效应一般定义介质是静止的，在坐标系的选择上，也是选择介质作为参考系。但萨格纳克效应不同，一般定义观察者或波源是静止的，在坐标系的选择上，可选择观察者作为参考系，但这两种效应的本质是相同的。多普勒效应一般应用于频率或波长的变化，而萨格纳克效应一般应用于传播时间或传播速度的变化。

A. 声波中的萨格纳克效应

光与声是一样的，只要是光波中所具有的性质，声波中也同样具有。超声波测量风速实际上利用的就是萨格纳克效应，它的基本原理是：超声波在空气中传播时，顺风与逆风方向传播存在一个速度差，当传播固定的距离时，此速度差反映成一个时间差，这个时间差与待测风速具有线性关系，通过测量两个方向上超声波到达时间，即可得出超声波在顺风和逆风下的传播速度，经过计算即可得到风速值。

当介质的运动速度相对观察者为v时，波从A点到B点所需要的时间，减去当介质相对观察者静止时波从A点到B点所需要的时间。也就是说，萨格纳克值就是由于介质的运动所产生的时间差。当介质的速度方向与波的传播方向存在夹角时，速度值取它在传播方向上的投影（余弦值）。

如图4-6所示，A点是声源，B点是观察点，AB两点的距离为L，介质速度为v，波的传播速度为c。

                                图4-6.声波中的萨格纳克现象

当介质相对观察者静止时，从A传播到B的时间为T=L/c，如果介质速度为v，其传播速度就是静态传播速度与介质速度的矢量叠加，从A传播到B的时间为t=L/(c+v)，当介质速度的方向与传播方向相同时，可以得出萨格纳克值为，相反时为

。例如，利用超声波测量风速过程中，已知c= 340 m/s，L= 0.1 m，如果测量出顺风与逆风的时间差Δt= 0.01 ms，则顺风与逆风的时间差就是上述两个正反相时萨格纳克值的差：，由于c>> v，可计算出风速= 5.78 m/s。

B. 光波中的萨格纳克效应

如图4-5所示，假设环路是边长为a的正方形，环形干涉仪以中心为原点，以角速度ω顺着光的传播方向旋转，如果以观察者（接收点）为参考点建立坐标系，则光路上的介质（以太）在光传播方向上的速度为v=-0.5ωa，如果以介质（以太）为参考建立坐标系，则光源和接收点在光传播方向上的速度为v=0.5ωa。不论以哪种参考系，波的传播速度都可表示为c-v。当环路相对以太静止时，光传播所需要的时间为T=4a/c，以角速度ω旋转时，光传播所需要的时间为t=4a/(c-0.5ωa)，萨格纳克值可表示为，正反向传播的时间差为。例如：如果a= 1m，ω= 1 rad/s，则环形干涉仪的萨格纳克值Δt= 2.22×10^-17 s，正反向传播的时间差为4.45×10^-17 s。

C. 中日双向时间传递中的萨格纳克效应

这个实验数据是中国国家授时中心同日本合作而测量出来的，中国的实验地点在西安（A，北纬 35.68°东经 139.75°），日本的实验地点在东京（B，北纬 34.27°东经 108.9°），地球同步卫星C在地球赤道上空， 距地心42100 公里，如图7-9所示。

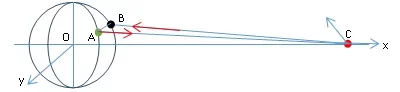
                                 图4-7.中日双向时间传递实验

图中的XOY面为赤道面，为了计算方便，假设C点和B点的经度相同，可以计算出从A到B的直线距离AB= 2800 km，BC= 37000 km，AC= 38000 km，∠ACB= 0.07 rad = 4°。

如果地球同步轨道内的以太与地球同步旋转，则从A点发射的电磁波经C点传播到B点时，萨格纳克值为0，但从3.1.2节的描述可以看到：只有高度在100公里内的以太与地球同步，也就是说，假设中转卫星定点于地球表面上空100公里处，无论电磁波的传播方向与地球自转方向是否相同，所得到的萨格纳克值都是0。当高度大于100公里时，以太的旋转速度逐渐降低，在距地面36000公里的同步轨道上，在月球的拖动下，以太相对地心的旋转速度只有91 m/s，如图3-2所示。

以地球中心为参考点建立坐标系，同步卫星静止于C点，可以求出以太在C点的速度约为-3000m/s，方向与B点的切线方向平行，负号表示与地球自转的方向相反。在C点上，由于∠ACB= 0.07 rad ，可以求出以太的速度在传播路径上投影为-208 m/s，由于以太相对于球心点的速度与距离成正比，因此，可以求出在电磁波的传播路径AC上任一点（距地球表面大于1000公里）以太的速度，在AC上的投影都等于-208 m/s。因此，电磁波从A到C传播时所产生的萨格纳克值可表示为，把L= AC- 200000= 3.78×10⁷ m，v= 208 m/s代入可得：Δt= 87.5 ns。由于电磁波从C到B传播时，以太的运动方向与传播方向垂直，BC段的萨格纳克值为0，因此，从A经C到B的总萨格纳克值为 87.5 ns。

可见看出：声与光的萨格纳克效应原理完全一样。

4.3.4. 波的反射与透射比较

A. 声波的反射与透射系数

如图4-8所示，平面界面两侧是两种介质：介质1和介质2，密度、声速和特性阻抗分别为

ρ₁、ρ₂，c₁、c₂，z₁、z₂，其中z₁=ρ₁c₁，z₂=ρ₂c₂，介质1中有一角频率为ω的平面波入射到界面上，它的传播方向与界面的法线成α角，透射方向与界面的法线成β角。

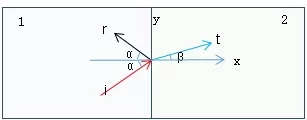
                              图4-8.声波的反射与透射

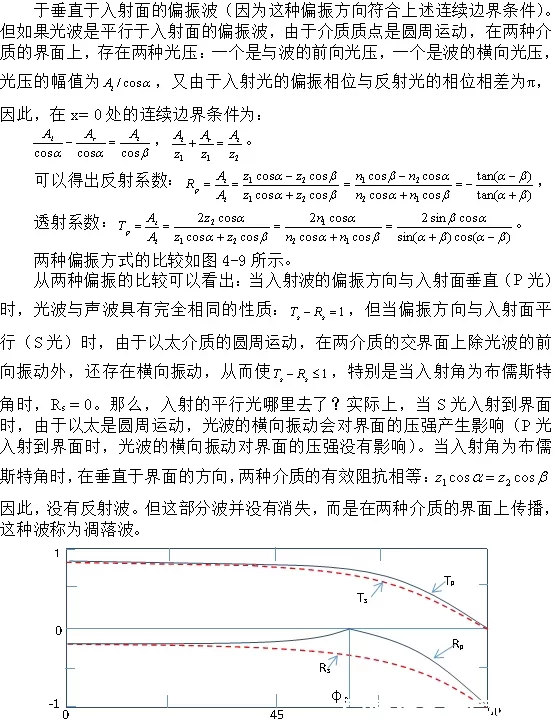
                                   图4-9.两种偏振方式的比较

上面的这四个公式，是菲涅耳当时是在研究弹性波如何通过二媒质界面这一问题时推导出来的，他的推导是建立在以太说的基础上，是远在麦克斯韦方程组之前就推导出了这套公式，我没有找到菲涅尔的原始推导过程，现代理论认为菲涅耳的以太理论基础是错误的，应该以麦克斯韦电磁理论为基础，但是，麦克斯韦电磁理论是“场”的理论，与“波”是风马牛不相及。

根据声与光的反射与透射比较，可以清楚地看出以太的存在。

4.3.5. 波的衰减比较

波的衰减一般包括扩散衰减、散射衰减和吸收衰减。

扩散衰减是指由于波束的扩散，随着传播距离的增加，波束截面越来越大，从而使单位面积上的能量逐渐减小。扩散衰减主要取决于波阵面的几何形状，与传播介质的性质无关，以太与空气具有完全相同的扩散衰减性质。

散射衰减是指波在传播过程中，遇到不同阻抗介质时发生散射，使波在原传播方向上的能量减少，散射并不吸收能量，而只是改变波的传播方向。散射主要分为三种：当粒子的尺度远小于波长时，所产生的散射称为瑞利散射，其散射强度与波长的四次方成反比；当粒子的直径与辐射的波长相当时的散射称为米氏散射，散射的强度与波长的平方成反比；当粒子的直径远大于辐射的波长时，称为无选择性散射，此时的散射与波长无关。声波与光波也具有几乎相同的散射性质。

吸收衰减是指波在介质中传播时，由于介质质点间的内摩擦（粘滞性）和热传导等因素，使波的能量转换成其它能量。空气具有一定的粘滞性，其吸收衰减与频率的平方成正比，超声波在空气中的衰减主要就是吸收衰减，例如，如果10 KHz的声波在空气中可以传播160多米，同功率40 KHz的声波只能传播10多米，1MHz的声波只能传播几厘米。但以太粒子间没有作用力（万有引力可忽略），其粘滞性可以忽略不计，可以认为以太没有吸收衰减，但如果以太中存在其他原子，当光波经过时，会引起原子的振动，从而产生吸收衰减。

吸收衰减中还有一个重要的衰减，本文称为共振吸收衰减，指的是介质中含有能够与波产生共振的粒子时所产生的衰减。例如，太阳光中的吸收谱线，自由电子的共振吸收等。一般金属在可见光波段与红外波段有极强的吸收性质，而且吸收带很宽，这种吸收就属于自由电子的共振吸收。萤石、氯化钠、氯化钾等晶体在22.9～63μm的红外波段内有强的吸收峰，这种吸收就属于原子的共振吸收。声波也存在共振吸收，在室内装修时，由于多孔吸声材料对低频声吸声性能较差，一般采用共振吸声原理来解决低频声的吸收问题。

可见，声与光的衰减性质几乎是相同的，但以太与空气的物理性质有一定的差异，主要表现在介质的吸收衰减上，这是由介质的性质决定的。

4.3.6. 声波也能在以太中传播

2019年12月，《自然》杂志报道了一项足以撕掉全世界物理课本的研究：声音能够在真空里传播！加州大学伯克利分校的Zhang lab在巧妙设计的实验装置的帮助下，首次观测到了声音在真空中传播的现象。

既然以太无处不在，为什么以太不能传播声音呢？实际上，以太完全能够传播声音，例如：所谓的“引力波”实际上就是天体运动所产生的以太振动，即使相隔几万光年也能传播到地球上。

在低频的情况下，以太确实没有空气传播振动的能力强。在介质中，体积元的能量可表示为：，可以看出：如果波的频率和振幅相同，介质的密度起到决定性的作用，由于空气的密度是以太密度的一百万倍，决定了低频情况下，以太传播声音的能力比空气弱一百万倍。

在我们的生活中，以太对声音的传播几乎没有作用，但声音确实能够在以太中传播，如果声音的频率达到1 MHz，以太对声音的传播能力将大于空气。因此，不是以太不能传播声波，而是以太对低频振动的传播能力太弱。

本文由奇点天文作者上传并发布，奇点天文仅提供文章投稿展示，文章仅代表作者个人观点，不代表奇点天文立场。