
6.1. 以太能作为光的载体吗?
6.1.1. 成也光败也光
把以太最早引入物理的是笛卡尔,他认为物体间不存在超距作用,物体之间的作用力都必须通过以太来传递,并建立了以太旋涡说,以此解释太阳系内各行星的运动,但这套理论并没有得到大家的公认。
1655年,胡克提出了光的波动说,他认为光的传播与水波的传播相似,后来惠更斯进一步发展了光的波动说。波必须在介质中传播(没有介质不能称为波),而这种介质就称为波的荷载物,如空气就是声波的荷载物。由于光可以在真空传播,因此惠更斯提出:荷载光波的媒介物质就是以太,它应该充满包括真空在内的全部空间,并能渗透到通常的物质之中。
在19世纪,以太观念才真正展现威力。托马斯·杨提出了光的波动说理论,以波动说成功地解释了光的干涉、衍射等现象,著名的杨氏双缝干涉实验,为光的波动说奠定了基础。继托马斯·杨之后菲涅耳再次证实了光的波动性,他提出的理论方法能正确地计算出衍射图样,并且能解释光的直线传播现象和光的双折射,也能计算出光的反射系数和透射系数,因此获得很大的成功。在托马斯·杨和菲涅耳之后,光的波动说就在物理学中确立了它的地位,以太论也获得了大家的认同,因此,19世纪大多数物理学家相信以太的存在。
但是,因为托马斯·杨和菲涅耳假定光是横波,而且实验也表明没有纵光波,但弹性媒质中除横波外一般还应有纵波,这就必然要求有一种弹性固体的以太。光学对以太性质所提出的要求似乎很难同通常的弹性力学相符合。为了适应光学的需要,人们要对以太假设一些非常的属性,例如,斯托克斯和开尔文提出:以太就像鞋匠的擦线蜡,它既可以发生振动(如激烈打击之下),又塑性地允许重物穿过它缓慢运动,但是,它的存在又如何对天体的运动毫无阻碍呢?
由于人们对以太的性质无法理解,光的横波理论又成为否定以太的证据。
6.1.2. 横波、纵波与偏振波
在我们的教科书中,波分为纵波和横波,纵波是指振动方向与传播方向一致或平行的一类波,即媒介(质点)的运动方向同波的运动方向相同或相反,横波是指质点的振动方向与波的传播方向垂直。例如,地震波就分为纵波和横波,空气中的声波是纵波。
但是,这种定义方法是欠妥的,难道自然界中就只有纵波和横波吗?介质质点的运动方向即不与波的传播方向平行、也不垂直的波是什么波呢?
在固体介质中,由于介质存在切向力,质点的横向运动可以引起附近的质点的横向运动,这就是横波。
但在流体介质中,切向力不复存在,质点的运动采用的是补位方式,当介质中出现空缺时,周围的介质就会向空缺处运动,如图6-1所示,从而形成质点的振动传播(即波)。
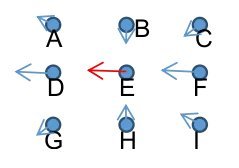
图6-1. 质点的运动方式
假设没有振动时,介质是均匀的,也就是质点的分布是均匀的,当质点E向D运动时,这个位置就会出现空缺,那么,邻近的质点就会向那里运动去替补这个空缺,并不是只有F点去替补,B点和H点也会向E点运动,只是幅度比较小,A、C、G、I这四个点也会存在轻微的运动。这种波可以称为纵波,其主要的传播方向是D(或F),但在B(或H)方向上,也有波的传播,只是幅度较小。即使是纯正的纵波,也不是所有质点的运动方向都与波的传播方向平行。
物体在空气中运动时,总会使空气的密度产生波动,运动物体的前方挤压空气使空气的密度变大,后方带动空气,使空气的密度变小。例如,汽车在空气中运动时,就会产生尾流,尾流是从多个方向流入的,并不是只从后方补充,高速列车运动时,头部区域附面层为圆球状,随着向车体截面过渡,列车侧面附面层逐渐变厚,到达列车尾端时,会出现显著变化,类似圆球状,接着过渡为逐渐扩张的圆管状。
从上述过程可以看出:在流体中,波在传播时,在波的传播方向上一定存在质点的运动(质点在波传播方向上的速度矢量不能为0),如果在某一个方向上没有质点的运动,波也一定不会向这个方向传播,也就是说,流体中横波不存在。例如,在上图中,如果质点B不存在上下振动,不论E点的振动幅度有多大,波都不会向B点的方向传播,因为E点的左右振动,并不能引起B点的左右振动,只能引起上下振动或椭圆运动,但幅度较小。这样的波本文称为偏振波,定义偏振波为:介质中质点的轨迹为椭圆的波。
综合上述分析:流体中的波都是偏振波,不存在横波。
6.1.3. 波的分类
波如何分类呢?实际上,所有的波都是偏振波,包括固体介质中的波,也就是说,任何介质中质点的运动轨迹都是椭圆。这里引入偏振度P的概念,并定义偏振度为:质点在垂直于传播方向上与平行于传播方向上的振动幅度之比。当P等于0时,为纵波,当P等于1时,为圆偏振波,当P等于无穷大时,为横波。偏振波可以包含自然界中大多数的波,纵波和横波只是偏振波的两个特殊形式。在纵波中,只有在波传播方向的中轴线上,质点的运动轨迹才是直线,其他方向上质点的运动都是椭圆,如图6-2表示。

图6-2. 纵波中只有中轴线上质点的振动方向与传播方向一致
在横波中,由于剪切力的存在,质点主要是横向运动,但也存在纵向运动。例如,在地震波中,即使波源完全是横向运动,也只有震源的正上方,质点的振动方向与波的传播方向垂直,只要偏离震源,波向外传播时,就包含有纵波,质点的轨迹就是椭圆运动。横波与纵波的传播速度不同,因此,在地震波中,即使在完全相同的介质中,地震波的速度也随着与波源距离的不同而不同。
水面波就是典型的偏振波,水分子的运动轨迹就是椭圆,有的教科书中把水面波称为横波,但水分子的运动方向与波的传播方向并不垂直,而是不断地变化。在无限深液体自由表面进行波中,液体质点围绕各自平衡位置作圆周运动,其半径在自由表面上等于波幅(偏振度为1),随质点所处自由面下的深度而按指数律递减(如图6-3a)。有限水深和浅水中的进行波,其流体质点运动的轨迹为具有水平长轴的椭圆(偏振度小于1,如图6-3b)。椭圆的长轴和短轴都随质点所处自由面下的深度而递减,短轴比长轴递减得更快;短轴在自由表面上等于波幅,递减至底面时为零,水愈浅,椭圆愈扁,偏振度越小(部分摘自百度百科:液体自由表面波)。
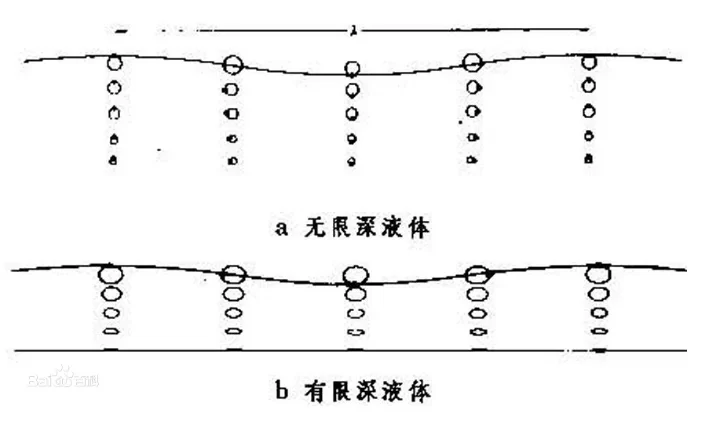
图6-3. 水面波(图片来自于百度百科)
在自然界中,很少存在单纯的纵波或横波,即使波源是单纯的纵波,波在传播过程中,并不是所有的质点都与波源的振动方向完全一致。如果单纯的纵波存在,波就不会发散,就是理想的平面波。
可见,自然界中最常见的是偏振波,有些教科书中无法定义水面波的原因,就是由于其质点的运动方向既不与传播方向平行也不垂直。在实际的横波中,质点的运动方式并不是与波的传播方向完全垂直,只是偏振度很大。在流体中,不能传播偏振度大于1的波,也就是说,流体中可以传播偏振度等于或小于1的波,这就为以太的存在扫除了最大的障碍。
6.1.4. 为什么光波中没有纵波?
在光传播方向的中轴线上也不存在纵波,这是事实,其原因是微观粒子的振动方式与宏观物体有所不同。对于宏观物体,由于是原子的整体运动,而且它的振动是由外力产生的,例如,锣不敲不响,而外力是有方向性的。但微观粒子不同,微观粒子的振动并不需要外力,例如,任何大于零K的物体都能发光,不需要任何的外力,也就是说,微观粒子的振动没有方向性,微观粒子发光时,其方向性也是随机的。
光波中为什么没有纵波呢?主要是由于粒子发光的同时存在横向振动,如果与声音类比,相当于我们一边走一边敲锣,从而使波传播方向上的中轴线不复存在。水面波之所以是偏振波,就是因为波源的振动方向与传播相垂直,也就是波源存在横向运动。这部分的内容将在光的产生一节中详细讨论,这里举一个例子来说明粒子在光的产生过程中的运动。
自由电子激光器所产生的光是线偏振光,其产生过程如图6-4所示。
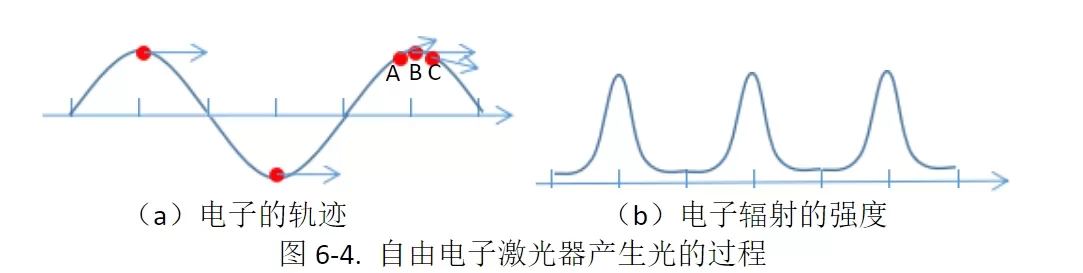
在自由电子激光器中,电子在荡波器中的运动轨迹类似于正弦(如图6-4a),由于电子的辐射强度与电子的急动度成正比,因此,电子所产生的波形是脉冲状,类似于正态分布(如图6-4b)。电子的运动可以分解为水平和垂直两个分量,水平分量比垂直分量大很多倍,水平分量主要作用是产生光,也就是使以太的密度产生变化(以这种方式产生的光是单向的),而垂直分量主要作用是产生偏振(也就是电子在产生光的过程中具有横向运动)。这种波在以太中是如何传播的呢?当电子在A、B、C三点时,由于发光的方向是电子运动的切线方向,光的传播速度比电子的运动速度快,A点所产生的光的相位比B和C提前,这三个点所产生的光会在以太中叠加,使以太粒子的运动轨迹为椭圆形,形成偏振波,其偏振方向与电子运动的轨道平面平行,其传播方式与水面波类似。
6.1.5. 小结
从上述讨论可以看出:光不是横波(指的是偏振度远大于1的波),是偏振度不大于1的波,以太完全能够作为光的载体,只要以太具有理想气体的性质即可,而不需要再给以太增加任何其他的性能。光就是机械波,具有机械波的性质,光波与一般宏观物体所产生的机械波的唯一不同之处就是:光的波源存在横向运动。光波是否偏振、偏振方式、偏振方向等只与波源有关,而与传播介质无关。
6.2. 光的产生
声音是物体振动产生的,但光是如何产生的却存在不同的观点,最流行的理论就是电子跃迁发射光子理论,该理论认为:光是由电子从高能量状态跃迁到低能量状态时,所失去的能量转化为光子。但是,电子是如何跃迁的?电子的能量是如何转化为光子的?光子的速度是如何获得的?光子是什么?如果电子跃迁一次只产生一个光子,如此多的光子是从哪里来的?一系列的疑问却没有答案,因此,这个理论是值得怀疑的。
本文认为:光与声音一样都是由物体(或粒子)振动产生的。从原理上,任何在以太中运动的粒子,都可以产生光,不论粒子是否带电。光和电磁波的关系,与声波和超声波的关系一样,光是高频电磁波。
6.2.1. 微观粒子的振动规律
微观粒子的常规运动一般可分为三类:1、直线运动,2、园周运动,3、简谐运动。
当粒子以速度v直线运动时,德布罗意假设粒子前进的波长λ满足![]() ;当粒子以速度v圆周运动时,玻尔假设粒子运动的周长l 满足
;当粒子以速度v圆周运动时,玻尔假设粒子运动的周长l 满足![]() ,即
,即![]() ;当粒子以角频率ω简谐运动时,本文假设粒子的振动幅度A满足
;当粒子以角频率ω简谐运动时,本文假设粒子的振动幅度A满足![]() ,其中,m是粒子的质量,h是普朗克常数。
,其中,m是粒子的质量,h是普朗克常数。![]() 是约化普朗克常数。
是约化普朗克常数。
如果仔细推敲这三个假设,其本质应该是相同的,其原因可能是粒子运动时存在共振。
6.2.2 光的产生方式
本文认为:光是由粒子振动产生的,自然光的产生主要有三种方式:
一是简谐振动发光,其特征是粒子以角频率ω简谐振动,发光强度与振幅的平方成正比,光的频率与粒子的振动频率相同,发光方向与粒子的振动方向相同,固体的发光属于简谐振动发光;
二是轫致发光,是粒子的运动突然转向时所产生的,粒子所辐射的光能量与它的急动度(加速度对时间的微分)成正比,发光方向与粒子速度的切线方向相同,原子的发光就属于此类(其特征是:电子的椭圆轨道运动),X射线谱也属于此类;
三是运动发光,是粒子在以太中的运动所产生的,发光方向与粒子的速度方向相同,这种方式所产生的波的能量很弱,气体发光就属于此类,只有当粒子的速度接近光速时,粒子所辐射的能量才比较明显。
下面举几个例子说明光的产生过程:
A. 直线运动
如果粒子在空无一物的空间中直线运动,是不会产生振动的,但是,如果粒子在流体中运动,在流体的作用下,粒子同样会产生振动,例如:在空气中直线运动的物体也会产生声音。微观粒子在以太中运动时,粒子振动的频率是它的固有频率,可表示为:![]() 。气体产生的辐射就可以看成是分子直线运动产生的,当粒子的直线运动速度与光速接近时,将会产生激波。自由电子激光器的原理与此相似,不同的是,自由电子激光器中的电子振动频率受到了人工的干预(自然的条件下,电子的振动频率是它的固有频率)。
。气体产生的辐射就可以看成是分子直线运动产生的,当粒子的直线运动速度与光速接近时,将会产生激波。自由电子激光器的原理与此相似,不同的是,自由电子激光器中的电子振动频率受到了人工的干预(自然的条件下,电子的振动频率是它的固有频率)。
B. 简谐振动
在固体中,原子的振动主要就是简谐振动,其振动方程可表示为:![]() ,在平衡位置,其速度(
,在平衡位置,其速度(![]() )最大,加速度(
)最大,加速度(![]() )为0,但急动度(
)为0,但急动度(![]() )最大。因此,简谐振动可以产生光,与简谐振动在空气中能够产生声音是同样的原理。粒子在平衡位置时所产生的辐射最大(与粒子的急动度成正比),所辐射的频率与粒子振动的频率相同,所辐射的方向与粒子速度的方向相同。
)最大。因此,简谐振动可以产生光,与简谐振动在空气中能够产生声音是同样的原理。粒子在平衡位置时所产生的辐射最大(与粒子的急动度成正比),所辐射的频率与粒子振动的频率相同,所辐射的方向与粒子速度的方向相同。
C. 圆周运动
圆周运动常见于电子的绕核运动。一般情况下,作圆周运动的物体都是匀速的,由于在圆周运动中,不论是切向加速度还是向心加速度都是常量,其急动度均为0,因此,正常情况下,圆周运动不产辐射。但是,如果粒子相对于以太的运动速度接近光速时,将会产生激波,与物体在空气中产生激波的原理相同,粒子所辐射的能量可表示为: 。其中r为轨道半径,β为粒子速度与光速的比值,E为粒子的能量,所辐射的方向是粒子运动的切线方向。
。其中r为轨道半径,β为粒子速度与光速的比值,E为粒子的能量,所辐射的方向是粒子运动的切线方向。
D. 圆锥曲线运动
圆锥曲线包括双曲线、抛物线和椭圆。当粒子进行圆锥曲线运动时,也能产生辐射,属于轫致辐射,常见于原子激态时外层电子的运动(主要是椭圆运动)、粒子间的碰撞(主要是双曲线运动)等,轫致辐射的能量同样与粒子的急动度成正比,当粒子距定点的距离最小时,辐射的能量最大,如图6-5所示。
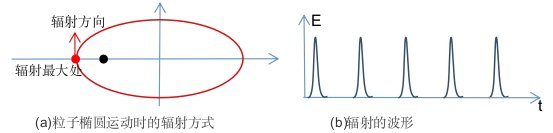
图6-5.粒子椭圆运动时的辐射
当粒子作椭圆运动时,粒子所辐射的频率等于粒子的轨道频率,所辐射的光是偏振的,偏振方向在轨道平面内,与长轴平行。
6.2.3. 热致发光
热致发光是最常见的发光形式,现在最流行的理论就是振动跃迁,但振动是如何跃迁的呢?没有人描述。任何物体只要温度相同,热致发光的频谱都是一样的,也就是说,光的频谱只与温度有关,而原子振动的频率也只与温度有关,与原子的类型无关。但是,怎样证明物体辐射的频率就是原子振动的频率呢?
当物体热致发光时,原子处于基态(核外电子都处于基态轨道上),可以把原子看成一个整体,不需考虑电子的作用。
证明物体辐射的频率就是原子振动的频率的思路:首先找出粒子最大动能密度所对应的振动频率,然后找出物体辐射的最大密度谱所对应的频率,如果两个频率相等,就可以说明。
A. 气体状态下的热致发光
根据麦克斯韦-波尔兹曼函数 ,由于F(v)的物理意义是:当温度T一定时,单位速度范围的粒子所占的比例数,因此粒子的动能密度分布函数可表示为
,由于F(v)的物理意义是:当温度T一定时,单位速度范围的粒子所占的比例数,因此粒子的动能密度分布函数可表示为
 ,平均动能可表示为
,平均动能可表示为
 ,其物理意义是加权平均值。令
,其物理意义是加权平均值。令![]() ,可得
,可得![]() ,也就是说,当
,也就是说,当![]() 时,粒子的动能密度最大。由于气体的辐射频率与气体粒子速度的关系为
时,粒子的动能密度最大。由于气体的辐射频率与气体粒子速度的关系为![]() (从
(从![]() ,
,![]() 得出),因此,当粒子的振动频率为
得出),因此,当粒子的振动频率为![]() 时,气体的辐射能力最强。
时,气体的辐射能力最强。
证明的第一步已完成,但最大密度谱所对应的频率比较难求,因为我们测量到的最大密度谱所对应的频率有两个,一个是以波长为单位的光谱辐射![]() ,其峰值符合维恩定律:,另一个是以频率为单位的光谱辐射
,其峰值符合维恩定律:,另一个是以频率为单位的光谱辐射![]() ,其峰值为
,其峰值为![]() 。
。
同一个辐射只能有一个最大值,怎么会出现两个最大值呢?之所以单位波长的峰值功率与单位频率的峰值不同,是由于所取的间隔不是常量造成的,因此,可定义单位频宽解决。
根据黑体辐射定律,单位波长的功率密度谱为 、单位频率的功率密度谱为
、单位频率的功率密度谱为 ,由于能量的辐射率
,由于能量的辐射率![]() ,因此,
,因此, ,定义
,定义 为单位频宽,则单位频宽的功率谱密度为
为单位频宽,则单位频宽的功率谱密度为 ,可以求出:单位频宽的功率密度最大时
,可以求出:单位频宽的功率密度最大时![]() 。可以看出,粒子的最大动能密度处的频率为
。可以看出,粒子的最大动能密度处的频率为![]() ,而辐射波的最大能量密度处的频率为
,而辐射波的最大能量密度处的频率为![]() ,二者并不相等,但相差不大,为什么呢?
,二者并不相等,但相差不大,为什么呢?
从上面的推导过程可以看出:粒子的最大动能密度处的频率采用的是麦克斯韦-波尔兹曼函数,而辐射波的最大能量密度处的频率采用的是黑体辐射定律,但黑体辐射定律是从固体的实验中总结出来的,难道固体的黑体辐射定律与气体不同?假设气体单位频宽的黑体辐射符合 (本文称为维恩曲线),可以求出:单位频宽的功率密度最大时
(本文称为维恩曲线),可以求出:单位频宽的功率密度最大时![]() ,图6-6是两种曲线的比较。
,图6-6是两种曲线的比较。
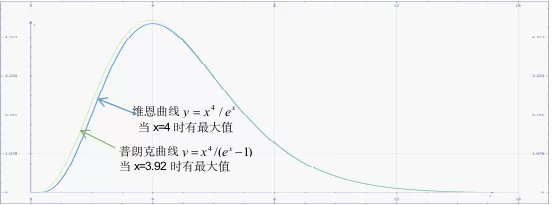
图6-6.维恩曲线与普朗克曲线的比较(Mathematics图)
为什么固体与气体所辐射的能量密度曲线会不同呢?
首先,实验用黑体都是固体(气体的辐射太弱),在固体中,原子并不是孤立的,原子间相互影响。可以猜测:如果不考虑原子间的相互影响,黑体的能量辐射谱符合维恩曲线,但当考虑相互影响时,黑体辐射符合普朗克曲线,也就是说,固体辐射符合普朗克曲线,而气体辐射符合维恩曲线。其原因可能是:由于原子共振时![]() ,原子的振动能量与频率成正比(振动能量
,原子的振动能量与频率成正比(振动能量![]() )。当温度一定时,由于振动频率高的原子振动幅度小,原子之间的联系性不强,其频率分布方式趋向于气体,但振动频率低的原子,它的振幅较大,结果是相邻原子之间的联系增强,也就是说,相邻原子振动的频率趋于一致,其振动频率的分布与气体有一定的差别。这可能就是维恩曲线与普朗克曲线在高频时相同,低频时有一定差异的原因。
)。当温度一定时,由于振动频率高的原子振动幅度小,原子之间的联系性不强,其频率分布方式趋向于气体,但振动频率低的原子,它的振幅较大,结果是相邻原子之间的联系增强,也就是说,相邻原子振动的频率趋于一致,其振动频率的分布与气体有一定的差别。这可能就是维恩曲线与普朗克曲线在高频时相同,低频时有一定差异的原因。
B. 固体的热致发光
对于固体如何证明原子的振动频率与它所辐射的频率相等呢?由于现代科技还无法直接测量固体中原子的振动频率和振动幅度,也无法知道原子的振动频率的分布规律,因此,无法求出原子最大能量密度处的频率,只能求出原子的平均振动频率。
由于固体中原子的平动和转动能量可以忽略,也就是说,原子只存在振动能量。设原子的振动方程为![]() ,则原子振动的能量为
,则原子振动的能量为 ,由于
,由于![]() (上文中的假设),可以得出每个原子的平均能量为
(上文中的假设),可以得出每个原子的平均能量为![]()
![]() ,由于固体的内能是由原子的振动产生的,根据能量均分定理,原子的自由度为3,因此,它的平均能量为
,由于固体的内能是由原子的振动产生的,根据能量均分定理,原子的自由度为3,因此,它的平均能量为![]() ,由此可得原子振动的平均频率为
,由此可得原子振动的平均频率为![]() 。在气体中,由于气体粒子的均方根速率为,粒子的平均平动动能为
。在气体中,由于气体粒子的均方根速率为,粒子的平均平动动能为![]() ,由于
,由于![]() ,可得出粒子的平均振动频率也为
,可得出粒子的平均振动频率也为![]() ,其平均动能也可表示为
,其平均动能也可表示为![]() 。可见,不管是固体还是气体,当温度一定时,粒子的平振动频率都是
。可见,不管是固体还是气体,当温度一定时,粒子的平振动频率都是![]() ,但粒子的最大动能密度处的频率稍有差别。
,但粒子的最大动能密度处的频率稍有差别。
固体辐射的平均(加权)频率是多少呢?
如果所分析的固体是一黑体,要想求出黑体所辐射的加权平均频率,就必须知道数密度分布。假设黑体所辐射的能量是由一个个能量为hf的光子所组成,当黑体的温度为T时,在单位时间、单位面积所辐射的总光子数为N。
由于单位频率功率密度谱 ,则单位频率内的光子数密度为
,则单位频率内的光子数密度为![]() 。设B(f,T)为光子数密度函数,归一化后可表示为:
。设B(f,T)为光子数密度函数,归一化后可表示为: ,则黑体辐射的平均(加权)频率可表示为
,则黑体辐射的平均(加权)频率可表示为![]()
![]() 。可以看出:固体中粒子的平振动频率与黑体辐射的平均(加权)频率并不完全相等,但也相差不大,其原因是:固体中的平振动频率是按照能量均分定理求出的,实际上,能量均量均分定理在固体中只是近似成立。如果气体的辐射符合维恩曲线
。可以看出:固体中粒子的平振动频率与黑体辐射的平均(加权)频率并不完全相等,但也相差不大,其原因是:固体中的平振动频率是按照能量均分定理求出的,实际上,能量均量均分定理在固体中只是近似成立。如果气体的辐射符合维恩曲线 ,可以计算出它的辐射平均(加权)频率恰好是
,可以计算出它的辐射平均(加权)频率恰好是![]() 。
。
C. 小结
对于热致发光,虽然没有严格证明光的频率就是原子振动的频率,但也相差不大。可以认为:气体的热致发光是原子运动产生的,属于运动发光,与电子无关,其辐射谱符合维恩曲线。固体的热致发光是原子振动产生的,也与电子无关(此时的电子处于基态)。原子所辐射的能量只与原子振动频率有关,而与原子的振动幅度无关。由于粒子振动方向是可变的,因此,能量是一份一份的。物体的辐射频率与原子的振动频率相等,原子的振动能量经过以太传播出来就是辐射,与声音的产生与传播原理是一样的。
温度与最大辐射能量密度时的频率及波长应该是对应关系,而且只能是一个,因此,对于黑体,本文定义:温度与峰值功率时的频率和波长关系为:![]()
![]() ,
,![]() ,不再区分
,不再区分![]() 和
和![]() ,例如:太阳的表面温度为5800 K,则太阳辐射的峰值频率为:4.375×1014 Hz,峰值波长为:6.33×10-7 m。
,例如:太阳的表面温度为5800 K,则太阳辐射的峰值频率为:4.375×1014 Hz,峰值波长为:6.33×10-7 m。
6.2.4. 激光的产生
学界主流对激光产生的描述仍然采用的是跃迁理论,但对原子处于某个能级时的物理状态则是只字不提,例如,核外电子的轨道参数等。如果电子处于不确定状态,它为什么会有确定的能量?因此,这种理论只能是一种假说。
本文认为:固体和CO2气体激光器中,激光的产生与电子无关(半导体激光与电子有关),是原子的共振引起的。
宇宙的大多数物质都是有弹性的,大到行星小到原子,几乎都能以一个或多个固有频率来振动。共振是物理学上的一个运用频率非常高的专业术语,不仅在物理学上运用频率非常高,而且共振现象也是一种宇宙间最普遍和最频繁的自然现象,所以在某种程度上甚至可以这么说,是共振产生了宇宙和世间万物,没有共振就没有世界。
A. 红宝石激光器
红宝石激光器是世界上第一台激光器,工作物质是红宝石棒,其基质是Al2O3,内掺有约0.05%的Cr2O3,Cr3+在晶体中取代Al3+位置而均匀分布在其中,在氙灯照射下,有波长为694.3 nm的激光输出。
传统理论认为:红宝石晶体中原来处于基态E1的粒子,吸收了Xe灯(波长为500 nm)发射的光子而被激发到E3能级。粒子在E3能级的平均寿命很短(约10-9秒)。大部分粒子通过无辐射跃迁到达激光上能级E2。粒子在E2能级的寿命很长,可达3×10-3秒。所以在E2能级上积累起大量粒子,形成E2和E1之间的粒子数反转,此时晶体对频率f满足hf= E2—E1(其中h为普朗克常数,E2、E1分别为激光上、下能级的能量)的光子有放大作用,即对该频率的光有增益。当增益G足够大,能满足阈值条件时,在部分反射镜端会有波长为0.6943微米的激光输出。
但是,红宝石晶体中处于基态E1的Cr2O3是什么状态?E2和E3又是什么状态?是怎样激发的?如何描述?为什么晶体对频率f满足hf= E2—E1的光子有放大作用?
本文认为:固体中的电子是很难存在激发态的,因为它没有足够大的空间,如果电子被激发,化学键就会被破坏,因此,固体发光只能是原子的振动,与电子无关。694.3 nm应该是与铬原子相联(由于红宝石是Al2O3掺杂Cr2O3的产物,Cr3+在晶体中只是取代Al3+位置而均匀分布在其中,与铬原子相联的氧原子同时也于铝原子相联)氧原子的伸缩振动的固有振动波长,而500 nm是只与铝原子相联的氧原子的伸缩振动固有振动波长。氙灯的照射只是增加了只与铝原子相联的氧原子的振动能量,因此,Al2O3只是起到能量的传递作用,但Cr2O3中的氧原子的共振波长与Al2O3中的氧原子的共振波长不同,从而导致这两种粒子有不同的振动频率。如果把Cr2O3振动形成的波再反馈回来,在以太的作用下,就可以形成众多Cr2O3粒子的同相共振,这就是激光,与空气中两个具有相同共振频率的物体能产生共鸣是同样的原理。
B. 二氧化碳激光器
在量子力学中,二氧化碳的发光被描述为振动能量的跃迁,但是,振动能量如何跃迁呢?振动能量跃迁就可以产生光子吗?没有人描述。
二氧化碳虽然是气体,但二氧化碳在产生激光的过程中,氧原子和碳原子都不存在激发态,二氧化碳也就没有激发态可言。CO2分子形状是直线形的,它的振动包括对称伸缩振动、不对称伸缩振动和形变振动,如图6-7所示。

图6-7.CO2分子的振动方式
如果说对称伸缩振动是基态,不对称伸缩振动是第一激发态,那么,从不对称振动变为对称振动就可以产生光吗?本文认为:二氧化碳的发光是简谐振动发光,1060 nm的波长就是不对称伸缩振动产生的,它是CO2的固有振动波长,与电子无关,所谓的振动能量跃迁纯属子虚乌有。
其辅助物质氦气,由于它容易被电离并在电场中被加速,能有效地提高粒子的动能。
辅助物质氮气,是作为动能的传递物,给二氧化碳提供振动的能量。
C. 自由电子激光器
传统理论认为:自由电子激光是通过自由电子和光辐射的相互作用,电子将能量转送给辐射而使辐射强度增大。
但是,自由电子是如何与光辐射相互作用的?电子又是如何把能量传送给光子的?一个速度慢的物体能够给速度快的物体传送能量么?
本文认为:当电子在扭摆器(或波荡器)中运动时,电子运动的轨迹类似于正弦波,如图6-8所示,当电子处于波峰时,急动度最大,辐射量也最大,辐射方向为电子运动的切线方向,属于典型的轫致辐射。自由电子激光是线偏振光,而且偏振方向在电子运动的平面内,并与电子的振动方向相同,这也是发光源横向运动的典型例子。
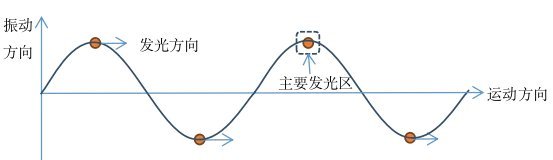
图6-8. 自由电子激光
电子所辐射的光是脉冲形式的,如果是单个电子,所辐射光的频率等于电子振动频率的2倍,但如果在一个周期内有n个间隔相同的电子,所辐射的光的频率就等于电子振动频率的2n倍,如果电子的间隔是随机的,所辐射的就不是单色光。
自由电子激光与半波天线的辐射方式相似,为什么半波天线所辐射的频率等于电子振动频率?这是因为接收方式的不同,在电磁波中,我们不仅能识别电流的大小,还能识别电流的方向,但在光波中只能识别光的强度,却无法识别以太介质的旋转方向(但可以通过偏振片识别振动平面)。
6.2.5. 太阳光的产生
太阳的大气通常可分为三层,分别为光球层、色球层和日冕层。
A. 光球层
光球层是如何发光的?主流认为:光球层的连续光谱主要是太阳大气中的负氢离子造成的,所谓负氢离子是指俘获一个电子的氢原子。但是,在高温环境中,氢原子发生电离,应该失去核外电子才对,怎么可能还俘获一个电子呢?因为只有俘获的电子,才能实现由外层高能级轨道向内层低能级轨道跃迁,释放能量,产生发射谱线,从这种解释就可以看出电子跃迁发射理论的缺陷(因为负氢离子在常温下并不能稳定存在,更别说高温了,在高温下,连氢原子都不能稳定存在,况负氢离子乎?我们不能用假想的离子去解释太阳的发光)。
太阳光球就是我们平常所看到的太阳圆面,其厚度约500公里,通常所说的太阳半径就是指光球的半径。本文认为:光球层发光属于气体(等离子态)状态下的热致发光,在太阳表面,氢原子基本完全电离。根据6.3.3节中的结论,对于热致发光,温度与峰值功率时的频率和波长关系为:![]() ,
,![]() ,不再区分
,不再区分![]() 和
和![]() ,太阳的表面温度为5800 K,则太阳辐射的峰值频率为:4.375×1014 Hz,峰值波长为:6.33×10-7 m。可以认为:在光球层中,等离子温度处于平衡状态,质子的速率分布符合麦克斯韦速度分布律,质子的平均速率为
,太阳的表面温度为5800 K,则太阳辐射的峰值频率为:4.375×1014 Hz,峰值波长为:6.33×10-7 m。可以认为:在光球层中,等离子温度处于平衡状态,质子的速率分布符合麦克斯韦速度分布律,质子的平均速率为![]() = 12 km/s。光球层的温度得到了大家的公认,没有人提出异议。
= 12 km/s。光球层的温度得到了大家的公认,没有人提出异议。
任何粒子,只要在以太中运动就能发光,与是否带电无关。光球层可能含有少量的氢原子,但不可能存在负氢离子,更不可能成为发光的主力军。光球层发光,主要是质子间的运动发光和质子间的碰撞所产生的轫致辐射,属于气体的热致发光。
B. 色球层
色球层是光球外面的一层,其发光比较复杂,包括热致发光(参见6.3)和原子发光(本文指的是核外电子在椭圆轨道上运动时,电子所产生的轫致辐射,参见6.5),在该层中,由于气体的温度较低,热致发光已退居次要地位,大气的主要成分也从离子态变为混合态(既有原子态又有离子态),大气的主要的发光形式也从质子碰撞(密度小时碰撞的几率小)发光转变为原子发光(电子与质子复合过程中的发光),因此,色球层中波长为6562.8埃的氢线Hα(共振线),在亮度上占绝对优势。
色球层的温度是有争议的,人们的一般常识是“离热源越近,温度越高”。但主流学者却认为:色球层离热源(太阳核心)越来越远,温度反而会越来越高。这一奇特现象已经困扰天文学家70多年,至今没有得到合理和公认的解释,因为离热源越远,温度越高是不可能的(当气体压强大于1帕时),它直接违反热力学定理。
为什么人们会认为在厚度约2000公里的色球层内,温度从色球底部的4,600K增加到色球顶部的几万度呢?这与人们的测温方式有关。由于我们不可能直接测量色球的温度,只能通过测量光的频谱来判断气体的温度。光源的温度常用色温这一概念来表示,光源发射光的颜色与黑体在某一温度下辐射光色相同时,黑体的温度称为该光源的色温,它是表示光线中包含颜色成分的一个计量单位。当黑体加热到一定的温度,它发出的光谱成分,就称为这一温度下的色温,计量单位为K(开尔文)。如果某一光源发出的光,与某一温度下黑体发出的光所含的光谱成分相同,就称为某K色温。如100W灯泡发出的光的颜色,与绝对黑体在2527℃时的颜色相同,那么这只灯泡发出的光的色温就是2800K,也可以说此时灯丝的温度就是2800K,这也是我们测量色球时所采用的方法。但是,用色温测量是存在条件的——物体必须是热致发光!其他的发光方式则不适用,例如,原子发光,它与气体的温度就没有直接的关系,在水银灯管中,色温可以是5800K,但管内的气体温度却不高。
色球层的发光是如何产生的呢?这是色球层中的独特运动形成的。色球是由许多细舌组成,被比喻成“燃烧的草原”,那上面许多细小的火舌在不停地跳动着,不时地还有一束束火柱窜起来很高。它最突出的特征是针状物,它是一个个的微型涡旋,在地球上称为“火龙卷”(空气中的高热引起的涡漩),即使是篝火,也会产生小规模的漩涡,地球上的火龙卷可以将15米或更高的树木连根拔起,其火柱可达100多米,相当于太阳上的日珥,如图6-9所示。正是这个涡旋产生的喷流才使氢原子的速度随着高度增加而增大。

图6-9.火龙卷(图片来源于网络)
需要指出的是:氢原子的速度随着高度增加而增大,指的是涡旋上方的局部区域,没有涡旋的区域,原子的速度是随着高度增加而减小。由于气体的温度与气体粒子运动速度的平方成正比,而气体的发光强度又与温度的4次方成正比,因此,我们所看到的只是温度高的那一部分,而温度低的部分却看不见。举一个例子,在一个1立方米的空间中,均匀地放置10根燃烧的蜡烛,如果从远处看,我们只能看到蜡烛周围的空气发光,根据光谱,我们可以判定这个1立方米空间中的空气温度为600 0C,但实际上,这个温度只是火焰周围的温度,而空气的平均温度可能只有40 0C。在色球中,一个针状物就相当于一根蜡烛。
可见,色球层中的温度下低上高可能只是一种假象,气体的平均温应该是随着高度的升高面下降。
本文认为:色球层的温度估计在5000—3000度之间。其原因为:首先,气体的温度不能太高,否则氢原子将会大量电离,所发出6562.8埃的氢线不可能很强,其次,温度也不能太低,否则氢原子电离太少,也不能发出较强的6562.8埃氢线。
C. 日冕层
主流认为:日冕层的温度也很高,原因可归纳为三点:
一、自1869年发现最强的日冕发射线波长为5303埃的绿线以后,多次日全食观测和日冕仪观测相继发现许多发射线,1942年,瑞典光谱学家艾德伦认为:日冕线属于极高度电离的离子产生的,最强的5303埃日冕绿线,是十三度电离的铁(Fe13+)产生的。
二、Fe13+产生的原因是由高温引起的,原子电离程度与温度有关,温度越高,粒子碰撞越激烈,越容易失去核外电子,计算表明,要想使日冕中的元素发生高度电离,需要一、二百万度的高温。
三、日冕的高温是太阳风形成的直接原因,如果日冕的温度没有这么高,那么太阳就不会发出太阳风。
但是,实际情况可能并非如此,原因如下:
1、最强的日冕绿线,不可能是Fe13+产生的
观测表明:日冕中物质的组成与太阳风是一样的,太阳风的主要成分是质子、电子和氦原子核(质子约占91%,氦核约占8%),氢和氦是太阳风的两大主要成分,这两种元素占太阳化学成分的99%。宇宙中几乎一半的重原子是氧,只有四种元素——氧、碳、氖和氮——占所有重原子的88%。因此,铁原子的含量非常低(地球大气中,铁原子只存在于尘埃之中),如果按照粒子的个数计算,铁离子的含量甚微,高度电离的铁离子可以忽略不计,它不可能产生如此多的发射线(认为Fe7+至Fe14+都能产生禁线,而且一种离子还可以产生多条禁线,例如:波长为6374和7892埃的发射线被认为是Fe9+和Fe10+的两条禁线等),更不可能成为最强的日冕发射线,而且,Fe13+是否能够稳定存在都是个问题,因为它吸收电子的能力非常强,我们在太阳风中并没有发现大量Fe13+的存在,铁原子也含量甚微。如果许多的日冕发射线都是铁离子产生的,在太阳风中应含有大量的铁原子。
我们知道,原子的光谱一般是固定不变的,但如果原子高速运动,它的核外电子的周期不可能不变(所产生的光谱也会变化),如果原子以更高的速度在以太中运动,其核外电子就无法存在(也就是电离)。因此,波长为5303埃的绿线很可能是氢原子在高速运动(一定速度范围内)状态下的共振波长(因为基态的氢原子在以太中高速运动时,电子的轨道不再是圆形,因此,基态原子在高速运动时也可能发射谱线),其他大部分的日冕禁线很可能都是氢或激态的氢或氦原子在高速运动状态下的谱线。
2、日冕的温度与太阳风的关系
由于我们测量温度的方法是光谱法,而光的谱线与粒子的速度有关,从3.2.3节对太阳风形成的讨论可以看出,太阳风是由涡旋产生的,与温度没有直接关系。

图6-10.古迪太阳望远镜获得的喷流成像图(图片来源于网络)
2014年8月1日,一个位于前导黑子附近,具有周期性的喷流重复发生了至少六次,其周期约为五分钟。美国大熊湖天文台的古迪太阳望远镜(GST)和太阳动力学天文台(SDO)卫星同时对这个喷流进行了观测。古迪太阳望远镜在氦10830埃波段获得了这个喷流的高分辨率成像图,图像呈现了目前为止喷流的最为清晰的精细结构,如图6-10所示。
从图中可以看出:除了喷流底部和倒Y型结构处的增亮,喷流其他部分均表现为吸收特征,说明了大部分的气体温度都很低。
美国太阳动力学天文台卫星(SDO)上搭载的大气成像望远镜(AIA)进行的观测显示,针状物上端出现了增强的171纳米辐射,表明高温只出现在针状物的上端。
同色球层一样,日冕层的高温也应该是一种假象,如果以原子的速度表示气体的温度,在日冕中,部分质子和电子(氢原子相对以太的速度大到一定程度时,电子会脱离质子而独立存在)可以被加速到200 km/s以上,根据![]() ,可以计算出质子的温度大于242万度,所发出的光频率大于
,可以计算出质子的温度大于242万度,所发出的光频率大于![]() = 1017 Hz(属于X射线)。但是,高速的原子只出现在喷流中,与气体总量相比,只占较小的比例。
= 1017 Hz(属于X射线)。但是,高速的原子只出现在喷流中,与气体总量相比,只占较小的比例。
3、温度是气体分子平均动能
温度只是表示物体冷热程度的物理量,微观上,是气体分子无规则(如果是规则运动,则温度与气体分子的平均速度关系不符合![]() )运动的剧烈程度,但是,这个运动的剧烈程度如何表示呢?对于固体,一般用原子的振动频率,而气体一般用分子的运动速度或者用分子运动产生的压强
)运动的剧烈程度,但是,这个运动的剧烈程度如何表示呢?对于固体,一般用原子的振动频率,而气体一般用分子的运动速度或者用分子运动产生的压强![]() 表示,其中,n表示单位体积内的分子个数。对于气体,在分子运动各向同性的情况下,这两种表示方法是一致的。但当气体中产生涡旋后,分子的运动速度不是各向同性,而且数值相差较大,分子运动速度高的地方色温高,气体的温度具有区域性,发光具有方向性。在龙卷风中,部分分子的速度也比较大,但平均温度却不高,色温与温度毕竟是两个不同的概念,色温可以是一点,但温度一般指的是平均值。
表示,其中,n表示单位体积内的分子个数。对于气体,在分子运动各向同性的情况下,这两种表示方法是一致的。但当气体中产生涡旋后,分子的运动速度不是各向同性,而且数值相差较大,分子运动速度高的地方色温高,气体的温度具有区域性,发光具有方向性。在龙卷风中,部分分子的速度也比较大,但平均温度却不高,色温与温度毕竟是两个不同的概念,色温可以是一点,但温度一般指的是平均值。
4、热成层是所有星体的普遍现象
热气流上升,对人们来说是常识,也就是说,动能大的分子向上运动。对于压强较大(大于1帕)的气体,当热气流上升后,压强降低,气体对外做功,温度下降,也就是说,动能大的分子向上运动后,动能将会下降。但对于压强较小的气体,由于气体上升后不再对外做功,因此,动能大的分子总是向上运动,也就是说,上面的温度总是高于下面的温度,这就是热成层,如图6-11所示。
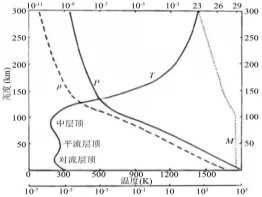
a. 地球大气温度随高度的变化
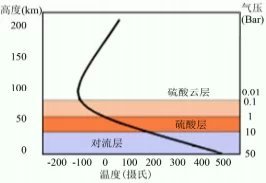
b. 金星大气温度随高度的变化

c. 木星大气温度随高度的变化
图 6-11. 星体的热成层(图片来源于网络)
地球大气的热成层受到太阳的影响很大,在太阳活动极大期的温度可 达 1600 K,但在太阳活运极小期约为 500 K 。比较有说服力的是海王星, 这颗行星的热成层有着大约 750 K 的高温, 要从太阳来的紫外线辐射获得 热量,对这颗行星来说与太阳的距离是太遥远了。热成层有一个共同的特 点: 每个星体的升温点基本都是在气体压强为 0.1 帕处。地球大气的 0.1 帕 处, 大致的海拔为 85~100 公里, 这也是为什么我们通常把 100 千米以上视 为气压为 0 了,而且常常以此为“太空”的界限(称为“卡门线”)。
日冕层,实际上应该是太阳的热成层,其以太的密度大于太阳大气的 密度,其平均温度可能在 105 K 之内,如图6-12所示。
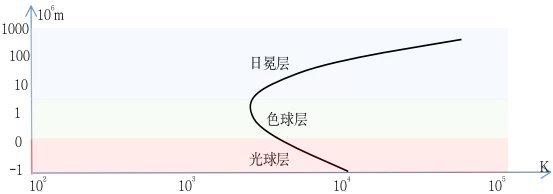
图 6-12. 太阳大气温度与高度的关系
6.3. 原子的光谱
6.3.1. 光谱产生的原理
与跃迁理论(该理论认为光是由电子的跃迁产生的)不同,本文认为:原子的发光是由于核外电子的椭圆运动产生的,属于轫致发光,是骤然改变物体的速度方向而产生的。电子在近核点的加速度最大,速度最高,发光也最强,发光方向为电子运动的切线方向。电子在不同的轨道上运动所发出的光的频率不同,但在基态或线系限轨道(指圆形轨道)上运动时不发光。电子每电离一次,在复合的过程中,都会发出一系列的光。电子椭圆运动时所发出的光是脉冲形式的(主要集中在近核区发光),但周期性的脉冲就是连续的光波,光的频率就是电子的轨道频率。只要电子在椭圆轨道上运动,原子就能发光,其发光强度与电子的急动度成正比。
6.3.2. 电子轨道与光谱的关系
A. 氢原子光谱
由于氢原子的引力系数(指的是电子受到的核引力相当于原子核的电荷数)恒等于1,它的线系限轨道的参数完全由角动量确定。第一激态的角动量为![]() (此时的轨道周期是基态周期的2倍),线系限轨道的速度
(此时的轨道周期是基态周期的2倍),线系限轨道的速度![]() = 1736316 m/s,半径
= 1736316 m/s,半径![]() = 84 pm,周期
= 84 pm,周期![]() =0.304 fs,能量
=0.304 fs,能量![]() = 8.57 ev。由于假设每个椭圆轨道的周期T与光谱值λ一一对应:
= 8.57 ev。由于假设每个椭圆轨道的周期T与光谱值λ一一对应:![]() ,例如:波长为121.6 nm的光谱与周期为0.406 fs的轨道是对应关系,假设同一个激发态中的轨道角动量都相等,也就是它们的正焦弦(也称为通径)都相等,可以计算出每个椭圆轨道的参数,如表6-6所示。
,例如:波长为121.6 nm的光谱与周期为0.406 fs的轨道是对应关系,假设同一个激发态中的轨道角动量都相等,也就是它们的正焦弦(也称为通径)都相等,可以计算出每个椭圆轨道的参数,如表6-6所示。
表6-1.氢原子的轨道参数与光谱
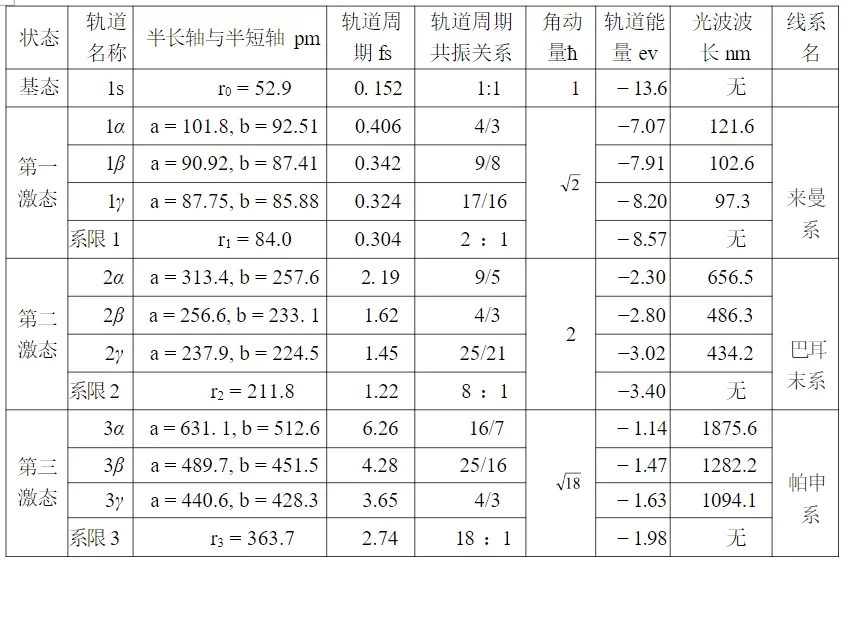
原子在基态时,电子是圆周运动,其轨道没有急动度,也就没有辐射,但当原子受激时,外层电子的轨道将产生偏心,从而产生光谱,它们的轨道示意图如图6-13所示,这里作如下假设:
- 每一个激发态对应一个线系;
- 同一个激发态中的轨道角动量都相等;
- 电子的每个椭圆轨道与光谱值都一一对应。
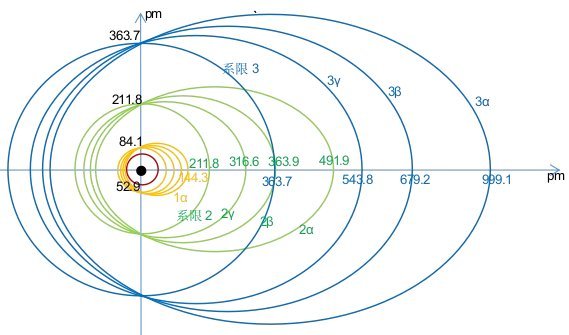
图6-13.氢原子的轨道示意图(红色是基态轨道,黄色为第一激态,
绿色为第二激态,蓝色为第三激态)
B. 氦原子光谱
- 第一激发态
当氦原子的一个电子被激发时,另一个电子的轨道也必然发生变动,由于外轨道电子对内轨道的影响很小,可忽略不计。因此,内轨道电子的速度![]() = 4.38×106 m/s,半径
= 4.38×106 m/s,半径![]() =26.5 pm,周期
=26.5 pm,周期![]() = 0.038 fs,能量
= 0.038 fs,能量![]() = -54.42 ev。
= -54.42 ev。
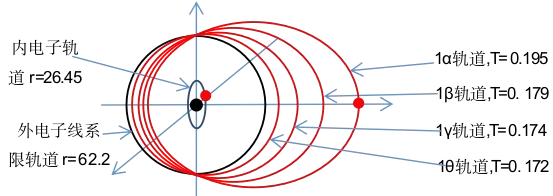
由于内外电子的运行轨道平面相互垂直(第一激发态的半径较小,内轨道电子对它的影响较大,如果不垂直,外轨道电子的能量将增加很多)。第一激态所辐射的四个波长分别为58.44 nm、53.71 nm、52.22 nm、51.56 nm,估计它的线系限波长为 50 nm。由于外电子的轨道处于第一激发态,其角动量是固定值![]() (相当于氢原子光谱中的来曼系)。可以得出第一激态线系限轨道的参数:周期
(相当于氢原子光谱中的来曼系)。可以得出第一激态线系限轨道的参数:周期![]() = 0.167 fs,速度
= 0.167 fs,速度![]() = 2.34×106 m/s,半径
= 2.34×106 m/s,半径![]() = 62.2 pm,能量
= 62.2 pm,能量![]() = -15.62 ev,引力系数X= 22/3r0/r= 1.35,其示意图如图6-14,轨道参数如表6-2所示。
= -15.62 ev,引力系数X= 22/3r0/r= 1.35,其示意图如图6-14,轨道参数如表6-2所示。
表6-2.氦原子轨道参数与光谱关系
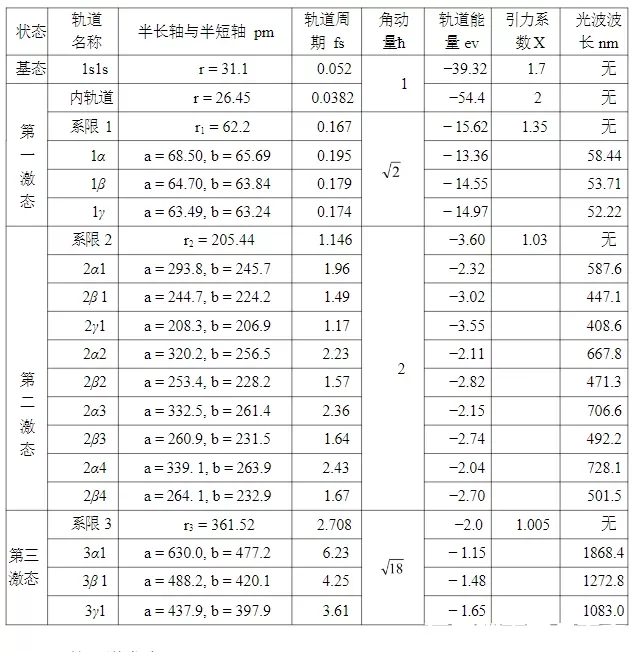
- 第二激发态
外轨道电子的第二激态比较复杂,其光谱相当于氢原子的巴耳末系,角动量为2ħ。根据几何原理可估算出线系限轨道的引力系数X= 1.03,周期T= 8T0/X2 = 1.146 fs(T0= 0.152 fs是氢原子基态周期),系限波长λ= cT= 343.56 nm,半径r= 4r0/X= 205.44 nm,由于轨道半径较大,外电子的轨道平面不会再与内电子轨道保持垂直关系,两个平面的夹角是随机分布的,正是内外电子轨道平面的夹角,才使轨道的近核点具有不同的引力系数,近核点的引力系数越大,辐射能力越强。设外轨道平面与内轨道平面的夹角为φ,大概可分为四种情况(这四种情况的线系限轨道半径相差不大):
- 当φ大于70度时,近核点的引力系数最大,这种情况出现的概率最高,光谱的强度也最大,轨道能量也最低。所对应的光谱波长为587.6 nm、447.1 nm、408.6nm。
- 当φ大于45度但小于70度时,所对应的光谱波长为667.8 nm、471.1 nm。
- 当φ大于20度但小45度时,所对应的光谱波长为706.6 nm、492.2 nm。
当φ小于20度时,所对应的光谱波长为728.1nm、501.5 nm。
- 第三激发态
其光谱相当于氢原子的帕申系,角动量为![]() ,系限轨道的引力系数估算为1.005,半径r= 361.52 pm,周期T=2.708,系限波长λ= 811.90 nm。由于轨道半径较大,外电子的轨道平面处于自由状态,可分为两种情况:
,系限轨道的引力系数估算为1.005,半径r= 361.52 pm,周期T=2.708,系限波长λ= 811.90 nm。由于轨道半径较大,外电子的轨道平面处于自由状态,可分为两种情况:
- 当φ较大时,所对应的光谱波长为1868.4 nm、1272.8 nm、1083.0 nm。
- 当φ较小时,所对应的光谱波长为2058.2 nm,其他光谱很弱。
C. 锂原子光谱
与氢和氦原子不同,由于锂原子外层电子的基态角动量是2ħ,它本身就是激发态,但由于受内层电子的影响很大,其运行状态可分为两类情况,第一类是线系限轨道就是原来的基态轨道,轨道平面与内电子轨道面保持平分关系,第二类是轨道平面与内电子轨道面不再保持平分关系,因此,线系限轨道向外转移,但其角动量不变,仍然是2ħ。为了与氢原子的光谱保持一致,本文规定:第一类为第一激发态,第二类为第二激发态。
- 第一激发态
锂原子的第一激发态的角动量为2ħ,所辐射的四个波长分别为671.01 nm、323.37 nm、274.22 nm、256.33 nm。线系限波长为229.97 nm,周期T= 0.767 fs,半径r= 168.13 pm,引力系数X= 1.26,称为主线系。
- 第二激发态
角动量仍然是2ħ,线系限波长为349.88 nm,线系限轨道的周期T= 1.167 fs,半径r= 207.3 pm,引力系数X=1.021。由于距核较远,外电子的轨道平面处于自由状态,不会再与内电子轨道面保持平分关系,又可分为两种情况:
- 当外电子轨道的长轴与内层轨道中轴线的交角较小时,所对应的光谱波长为610.54 nm、460.43 nm、413.36 nm、391.63 nm,由于轨道参数容易受到内层电子(主要是外层电子的近核点受内层顶点处)的影响,因此谱线发散,被称为漫线系。
2、当外电子轨道的长轴与内层轨道中轴线的交角较大时,所对应的光谱波长为812.95 nm、497.33 nm、427.45 nm、398.70 nm。由于内层电子的影响较小,被称为锐线系。
- 第三激发态
其光谱相当于氢原子的帕申系,其角动量为![]() ,线系限波长为819.50 nm,可计算出线系限轨道的周期T= 2.734 fs,半径r= 363.33 pm,引力系数X= 1.0003。由于距核较远,外电子的轨道平面处于自由状态,所对应的光谱波长为1870.21 nm、1278.56 nm、1090.33 nm。
,线系限波长为819.50 nm,可计算出线系限轨道的周期T= 2.734 fs,半径r= 363.33 pm,引力系数X= 1.0003。由于距核较远,外电子的轨道平面处于自由状态,所对应的光谱波长为1870.21 nm、1278.56 nm、1090.33 nm。
表6-3.锂原子轨道参数与光谱关系
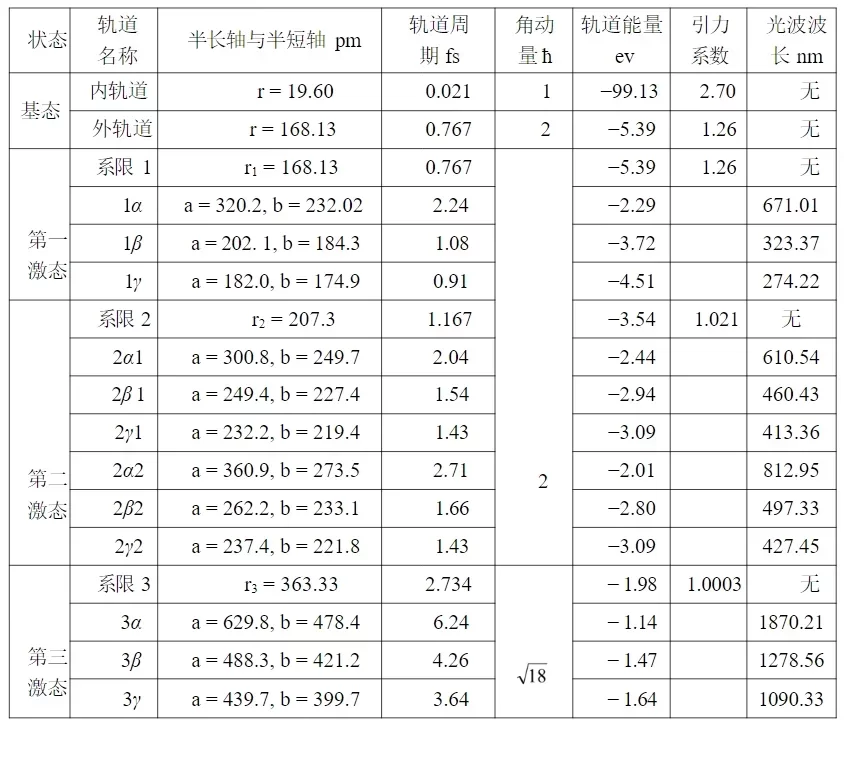
6.3.3. 原子光谱的规律
A. 第一激态
氢和氦第一激态的角动量为![]() 。除氢和氦原子外,所有原子第一激态的线系限轨道都是它的基态,其角动量都等于
。除氢和氦原子外,所有原子第一激态的线系限轨道都是它的基态,其角动量都等于![]() ,系限波长λ与轨道能量E的关系为
,系限波长λ与轨道能量E的关系为![]() ,例如:锂、钠、钾的外轨道能量分别为5.39 ev、5.14 ev、4.34 ev,可以计算出它们的第一线系限波长分别是229.92 nm、241.24 nm、285.59 nm,与实验值完全相同。其共振谱线(是指元素特征光谱中强度最大的谱线)也都在第一激态,因此也被称为主线系。第一激态的谱线比较简单,与锐线系的结构相似,原因是内层电子的影响较大,外层电子必须在内层电子屏蔽最低的空间内运行,也就是说:外电子轨道平面与内电子轨道平面的夹角保持不变(与基态时的角度一样)。谱线的双线结构是由于外层电子的轨道平面与内层电子中轴线的夹角不同引起的。
,例如:锂、钠、钾的外轨道能量分别为5.39 ev、5.14 ev、4.34 ev,可以计算出它们的第一线系限波长分别是229.92 nm、241.24 nm、285.59 nm,与实验值完全相同。其共振谱线(是指元素特征光谱中强度最大的谱线)也都在第一激态,因此也被称为主线系。第一激态的谱线比较简单,与锐线系的结构相似,原因是内层电子的影响较大,外层电子必须在内层电子屏蔽最低的空间内运行,也就是说:外电子轨道平面与内电子轨道平面的夹角保持不变(与基态时的角度一样)。谱线的双线结构是由于外层电子的轨道平面与内层电子中轴线的夹角不同引起的。
B. 第二激态
第二激态是最复杂的,但角动量都是![]() ,其原因是外层电子轨道的平面可以自由转动,但轨道参数仍受内层电子的影响。对于第一主族元素,可分为两种情况:第一种是外层电子的长轴与内层轨道的中轴线夹角较大,外层电子的近核点受到内层电子轨道顶点的影响较小,所表现出的谱线就是锐线系;另一种情况是外轨道长轴与内轨道的中轴线夹角较小,外层电子受到内层电子轨道顶点的影响较大,所表现出的谱线就是漫线系。不论是锐线系还是漫线系,轨道平面与内层中轴线的夹角也会影响到光谱,其表现就是谱线的双线结构,系限轨道也可分为两个,当轨道平面与内层轨道的中轴线的夹角较大时,轨道周期较小,夹角较小时,周期较大。
,其原因是外层电子轨道的平面可以自由转动,但轨道参数仍受内层电子的影响。对于第一主族元素,可分为两种情况:第一种是外层电子的长轴与内层轨道的中轴线夹角较大,外层电子的近核点受到内层电子轨道顶点的影响较小,所表现出的谱线就是锐线系;另一种情况是外轨道长轴与内轨道的中轴线夹角较小,外层电子受到内层电子轨道顶点的影响较大,所表现出的谱线就是漫线系。不论是锐线系还是漫线系,轨道平面与内层中轴线的夹角也会影响到光谱,其表现就是谱线的双线结构,系限轨道也可分为两个,当轨道平面与内层轨道的中轴线的夹角较大时,轨道周期较小,夹角较小时,周期较大。
对于氦原子和第二主族,由于一个电子受激时,另一个电子的轨道半径也发生变化,两个电子相互影响较大,所表现出来的就是两套线谱:估计当两个轨道的平面夹角大于25度时,表现出的是一套(漫线系),夹角小于25度时是另一套(锐线系)。在很多资料中把667.8 nm的谱线归到仲氦不一定正确,它应属于漫线系,只是它的谱线弱,在第二激态中,只有728.1 nm、501.5 nm两个谱线属于氦原子的锐线系。
对于多电子结构,更为复杂,一个电子受激时,其他电子的轨道半径和角度都变化,从而表现出复杂的谱线结构。
C. 第三激态
第三激态较简单,角动量为![]() ,对于第一主族及氦元素,由于外层轨道半径与内层相差较大,内层电子对外轨道参数的影响很小,其引力系数略大于1,其谱线与氢原子的第三激态相差很小(百分之1之内)。但对于其他原子,内层电子还有一定的影响,例如镁原子的第三激态,两个外层电子间影响还比较明显的,例如,它的第三激态波长为1503.2 nm、1029.5 nm、880.6 nm等,比氢原子的第三激态波长小很多,可以估算出此时的引力系数为1.11,系限波长为667.4 nm。
,对于第一主族及氦元素,由于外层轨道半径与内层相差较大,内层电子对外轨道参数的影响很小,其引力系数略大于1,其谱线与氢原子的第三激态相差很小(百分之1之内)。但对于其他原子,内层电子还有一定的影响,例如镁原子的第三激态,两个外层电子间影响还比较明显的,例如,它的第三激态波长为1503.2 nm、1029.5 nm、880.6 nm等,比氢原子的第三激态波长小很多,可以估算出此时的引力系数为1.11,系限波长为667.4 nm。
D. 其它激态
第四及以上的激态,与氢原子的谱线几乎完全一样,但除氢原子外,其他原子的谱线几乎无法测量。这是因为氢原子的谱线没有其他电子的干扰,而且电子的轨道平面在任何角度都是一样的,而其他原子的谱线不但和受激电子的轨道长轴与内层轨道中轴线的夹角有关,还和轨道平面与内层轨道中轴线的夹角有关,因而谱线是发散的,从而导致谱线太弱。
6.3.4.精细结构
在光谱学中是指原子的主要光谱线分裂为两个或更多个分量,每个分量表示的波长略有不同。物理学家们精确地研究了各种元素的光谱,并积累了大量的光谱数据。1891年,迈克尔逊通过更精确的实验发现,原子光谱的每一条谱线,实际上是由两条或多条靠得很近的谱线组成的。这种细微的结构称为光谱线的精细结构。
- 氢原子的精细结构
从原理上,任何原子都存在精细结构,因为电子的轨道总会受到其它各种因素的干扰,氢原子只有一个电子,没有其他电子的影响,但原子核的运动会对它的轨道参数产生影响,因此,任何谱线都有一定的宽度,原子运动所产生的多普勒效应会使谱线展宽。虽然主流认为氢原子的精细结构是相对论效应和电子自旋效应,但谁又能排除多谱勒效应的影响呢?
- 第一主族元素的精细结构
锂原子产生共振谱线时,由于激态电子的轨道恰好在内层电子轨道平面的平分线上(能量最低),而且内层电子的两个轨道平面垂直,每个电子的轨道平面都不发生转动,因此,锂原子的精细结构无法通过普通的分光镜分辨出来。
但钠、钾、铷等原子不同,它们的激态电子轨道平面与内层电子的平面没有明显的关系,也就是说,二者的夹角可以是任何值。由于内层电子轨道的中轴线上电子的密度稍大,当激态电子的轨道平面与内层电子轨道的中轴线的夹角较大时,所产生的谱线波长较小,反之较大,因此,共振谱线有明显的分裂。
可见,产生精细结构的原因是:内层电子对激态电子轨道的影响,主要是影响激态电子的轨道周期,漫线系的存在也是这个原因(漫线系光谱也属于精细结构)。氢原子的光谱原则上不应具有精细结构,因为没有其他电子的影响,它的谱线展宽很可能是多谱效应。
另外,除了激态电子轨道平面的角度变化会使谱线分裂外,即使激态电子轨道平面的角度不变,椭圆轨道近核点的变化同样会使激态电子轨道的周期出现微小的变化,这很可能就是光谱具有超精细结构的原因。
6.3.5. 小结
原子的光谱是电子绕核椭圆运动产生的,属于轫致发光,发光强度与电子的急动度成正比。原子的光谱与激态电子的轨道一一对应,其原因就是共振。电离能与光谱值都和电子的轨道紧密相联。
6.4. 光的传播
6.4.1. 光子并不实际存在
主流理论认为:光子是光线中携带能量的粒子,是传递电磁相互作用的基本粒子,是一种规范的玻色子。但在爱因斯坦晚年的时候,仍对光子的概念困惑不已,他说:“我认真思考了五十年,光子是什么?但是并没有找到答案”。证明光子存在的实验主要有光电效应和康普顿效应。在光电效应中,光表现为一颗一颗的光子打在金属表面上,一份一份的能量即被电子吸收,所以说光具有粒子性。但是如果假设光子是光线中携带能量的粒子,就会产生如下逻辑混乱:
A. 一个光子在空间上是一个点,还是一定范围的分布?如果是一个点,相干性就难以理解了,如果是一定范围的分布,那么多大范围?如何分布?为什么人们从来没观察到光子与光子相撞的现象!
B. 光子的频率越高,光通过三棱镜后的偏转角越大,但如果按照光子说则应该是:频率越高偏转角越小!因为频率越高的光子,动能或动量越大,改变方向的难度也就越大,因此,光的折射无法用光子进行解释。
C. 光在空气中的速度约为30万千米/秒,在玻璃中约为20万千米/秒。当光子从玻璃出来再次进入空气时,速度瞬时增加了50%,同时运动方向也发生了突变,这并不是粒子所具备的特性,也不符合动量守恒。
D. 如果光是粒子,在介质中,其速度应该会随运动距离的增加而降低,但光在均匀介质中的速度却是恒定的。
E. 任何黑体所辐射的频率谱在频率上都是连续的,根黑体辐射定理可以求出每Hz频宽内的辐射度,这种频率分布特性是无法用单一频率的光子来解释的。例如,天狼星是全天空最亮的恒星(太阳除外),它的总光度为9.77×1027 w,在地球上,每平方毫米能够接收到天狼星的光功率为1.18×10-13 w,如果换算成500 nm的光子,约为30万个。假设天狼星的频谱范围是200-800 nm,光子在这个频谱范围平均分配,可以计算出在1秒时间内,每间隔3.8×109 Hz才存在一个光子,但实际上天狼星的光却是连续的。同样的条件下,在地球上每平方毫米能够接收到太阳的光功率为1.36 mw,可以计算出每Hz才存在3个光子,如果接收的时间变短,每Hz存在的光子数更少,但不论接收太阳光的持续时间是多少,太阳光的频谱都是连续的。
F. 光的干涉和衍射现象都不能用光子解释,相位相反的光子叠加后,光子哪里去了?
G. 如果光是由光子组成的,单个光子的波动模式就无法理解(如果光子是波形运动,光子的实际运动路径的速度将大于光速,如果光子不波动,光的偏振就无法解释),半波损失就更不可理解了。
H. 证明光是粒子的实验并不能让人信服,例如,发生光电效应时,光的频率存在一个范围,随着光频率的升高,光电效应现象反而不明显,明显的是康普顿现象,这说明把光当作粒子是存在问题的。再如,在康普顿实验中,与电子水平相撞的光子,可以使电子获得比光子还要大的动量,最可疑的是这个电子还无法逸出(不发生光电效应)。
可见,光具有粒子性,但光并不是由光子组成的,因为光的所有性质,超声波都具有,如果产生超声波的源存在横向运动,超声波也会偏振。如果承认以太的存在,就没有光子存在的必要。
6.4.2. 光子与声子的比较
光是以太中传播的波,光子是假想的粒子,与声子(用来描述晶格的简谐振动)一样,是用来描述以太中体积元的简谐振动,光子不是一个真正的粒子,光子也可以产生和消灭。光子与声子的比较如表6-4所示:
表6-4.光子与声子的比较
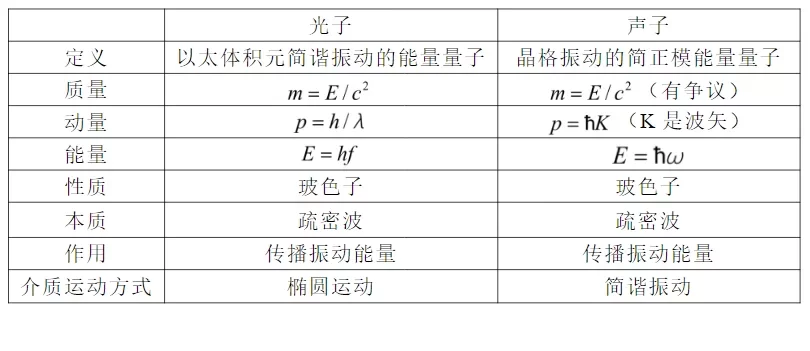
声子存在于微观的晶格之中。由于空气分子相距遥远,它们之间没有明显的弹性联系,不能形成集体激发,也就不能有效传递声子的振动。既然空气中没有明显存在的声子,为什么以太中能够存在光子呢?标准状态下,每立方米中空气中的粒子数为2.69×1025个(粒子间的平均距离为3.34 nm),而每立方米中的以太粒子数为1.8×1033个(以太粒子间的平均距离为8.22 pm),二者的比值为6700万。以太的静态压强为67800 MPa,而空气的静态压强为0.101 MPa,二者的比值为67万。晶格之间的紧密关联性是由于分子间的吸引力引起的,而以太粒子之间的关联性是通过巨大的静态压强实现的。实际上,空气中也存在声子特征,只不过没有在固体和液体中明显,如果空气的压强达到100 MPa,空气中粒子间的关联性也会增强,声子特征也将能够显现。
可见,光子可定义为:光波在以太中传播时所产生的疏密波,是以太体积元振动的能量,同声子一样,是一种准粒子。
6.4.3. 用波动说解释光子
如果以太不存在,波动说是无法解释光子的,但是,没有以太,光波也就不存在了。用电磁场理论去解释光子,显然是用未知来解释未知,因为我们并不知道电磁场是什么。在光子理论中,一面用表示波特征的波长和频率来表示光的动量和能量,一面又把光解释成粒子。我们不知道光子是什么,却有时把光子描述为可以与电子完全弹性碰撞粒子,有时又描述为电子可以完全吸收而产生跃迁的波,但吸收或跃迁过程却无法描述。当光子与电子相遇时,电子是在怎样的状态下把光子弹出?又在怎样的状态下把光子吸收?
假设以太存在,并且是光传播的介质,光子就很容易解释:
光是微观粒子振动产生的,在宏观世界里,物体的振动必须依靠外力,但在微观世界里,微观粒子的振动不需任何的外力,只要存在温度,微观粒子就会永远地振动下去,这就是物体的温度只要大于绝对零度,就存在辐射的原因。
微观粒子的振动规律是![]() (见第6.2.1节),而微观粒子的振动能量可表示为
(见第6.2.1节),而微观粒子的振动能量可表示为![]()
![]() ,也就是说,微观粒子每个振动周期的能量是
,也就是说,微观粒子每个振动周期的能量是![]() (在量子场论中,每个时空点都被看作是量子化的简谐振子,每个谐振子的真空期望值为0.5nh,其中n是自然数,这也可能是在普朗克新的辐射公式中存在零点能量的原因)。如果微观粒子通过以太把振动能量全部辐射出去,空间中每个波长的能量就是
(在量子场论中,每个时空点都被看作是量子化的简谐振子,每个谐振子的真空期望值为0.5nh,其中n是自然数,这也可能是在普朗克新的辐射公式中存在零点能量的原因)。如果微观粒子通过以太把振动能量全部辐射出去,空间中每个波长的能量就是![]() 。很明显,微观粒子所辐射的能量与它的振幅无关,而且光确实是一份一份的(因为粒子的振动方向会发生变化),每一份就是一个波长,其能量为
。很明显,微观粒子所辐射的能量与它的振幅无关,而且光确实是一份一份的(因为粒子的振动方向会发生变化),每一份就是一个波长,其能量为![]() ,这也是微观世界与宏观世界的主要区别。
,这也是微观世界与宏观世界的主要区别。
光电效应发生时,电子并不是被光子“撞”出来的,而是“振”出来的,这个过程可以与超声波清洗相比较(已在1.3.1节中作了详细介绍)。在光电效应中,被“振”出来的电子应该是在轨道运行的电子,而不是自由电子,因为只有与电子的轨道频率相近的光才能振出电子。这就是光电效应需要一定的时间(约10-9秒)和一定频率范围(只有某一频率范围的光才能产生较多的电子)的原因。
可见,光子可比喻成驻波中的波腹,是一个个传播着的能量包。
6.4.4. 康普顿散射的本质
康普顿在研究石墨对X射线的散射时,发现在散射的X射线中,不但有波长等于原波长的射线,而且还有波长大于原波长λ0的部分。但是,康普顿在解释这一现象时,却一直认为光就是波,因为解释康普顿实验(包括光电效应)的重点是波长和频率(假设光子的能量为![]() ,光子的动量为
,光子的动量为![]() )。这是因为当光的波长很短时,光的能量集中在一个点上,完全可以把光波的一个周期假想成一个光子,这个光子本质上就是一个波包,它具有粒子的性质。
)。这是因为当光的波长很短时,光的能量集中在一个点上,完全可以把光波的一个周期假想成一个光子,这个光子本质上就是一个波包,它具有粒子的性质。
6.5. 以太的传播性质
6.5.1. 为什么光的传播介质只能是以太?
光波的传播只能依靠以太传播,其原因为:
A. 一般介质的吸收衰减太大
一般的物质都具有粘滞性,其原因是原子间都存在范德华力,这种作用力能对于波的传播带来很大的吸收衰减。例如,空气对超声波的吸收衰减与频率的平方成正比,如果频率为6×1014 Hz的光,以空气为介质传播,估计传播的距离不会超过1毫米。只有以太粒子间没有作用力,其吸收衰减可以忽略。
B. 单个粒子振动所产生的幅度太小
在微观世界里,粒子振动的规律是![]() ,例如,温度为300K的任何原子,其平均振动角频率为
,例如,温度为300K的任何原子,其平均振动角频率为![]() =1.17×1014 rad/s,可以求出原子的振幅为A= 3.15×10-12 m,在一般物质组成的介质中,如此小的振幅是无法叠加的,也无法形成波。
=1.17×1014 rad/s,可以求出原子的振幅为A= 3.15×10-12 m,在一般物质组成的介质中,如此小的振幅是无法叠加的,也无法形成波。
6.5.2. 介质中的光速
光在介质中传播时,为什么速度会减少?目前有三种观点:
- 光在玻璃中的速度还是真空中的速度,只是光在玻璃中碰撞到很多电子,多走了很多弯路,从而在宏观上速度变小了。
- 光是电磁波,玻璃中的电子吸收又释放,从而耽误了时间,导致速度变小。
- 光速是由磁导率和介电常数决定的。
但是光在由原子组成的介质中传播时,如果光在介质中碰撞到很多电子,或光被电子吸收又释放,则光波肯定是发散的。光速确实与磁导率和介电常数有关,但在电磁波中,磁导率的物理意义就是以太的密度,而介电常数就是以太的体积压缩系数。在电磁场中的介电常数与电磁波中具有不同的物理意义(电磁场中指的是分子的极化程度),例如:水的介电常数是78.36 F/m,但水的折射率却是1.33,在高频状态下,水分子的极化无法跟上电磁场频率的变化,极化程度也就无从谈起。
波在任何介质中的速度可表示为:![]() ,其中P表示介质的弹性模量。光波也不例外,由于光波传播的介质只有以太,其密度不变,因此,光在由原子组成的介质中传播时,其中的原子只能当作以太中的杂质,这些杂质的作用相当于降低了以太的弹性模量,或者说是增加了以太的体积压缩系数,或者说相当于增加了以太的密度(假设以太的弹性模量不变)。这些杂质不但阻碍以太的振动,还会吸收以太振动的能量,这才是光在由原子组成的介质中传播时,速度减少的真正原因。
,其中P表示介质的弹性模量。光波也不例外,由于光波传播的介质只有以太,其密度不变,因此,光在由原子组成的介质中传播时,其中的原子只能当作以太中的杂质,这些杂质的作用相当于降低了以太的弹性模量,或者说是增加了以太的体积压缩系数,或者说相当于增加了以太的密度(假设以太的弹性模量不变)。这些杂质不但阻碍以太的振动,还会吸收以太振动的能量,这才是光在由原子组成的介质中传播时,速度减少的真正原因。
6.5.3. 波的反射与折射原理
主流对波的反射和折射是用著名唯象理论——惠更斯原理进行解释的,惠更斯认为:波前的每一点可以认为是产生球面次波的点波源,而以后任何时刻的波前则可看作是这些次波的包络。借着这原理,他可以给出波的直线传播与球面传播的定性解释,并且推导出反射定律与折射定律。
但是,在任何均匀的介质中,同一个介质粒子的运动总在不断地变化着,但介质粒子的速度向其传播方向上的下一个介质粒子进行着大小不变的传播。空间中每一个介质粒子,在介质粒子密度产生的属性力的作用下,不断地发生运动速度的改变,但对于同一个介质粒子而言,无论其速度为多少,传播后一定能够使下一个粒子获得相同的速度,即介质粒子的速度在传播过程中不会发生突变。正是因为均匀介质中的介质粒子间的等速传播,并没有造成空间介质粒子新的不平衡的分布,所以,并不会因空间某个介质粒子的振动而形成新的波源,介质粒子还是传播着由原始振源产生的波动。
可见,波在均匀介质中传播时并不能产生次波,波前的每一点并不是产生球面次波的点波源,只有在两种介质的交界面上,才能产生次波。因此,惠更斯原理应该描述为:波源决定波的频率、偏振、强度和方向,介质决定波的速度和衰减,在两种介质交界面上的每一点,可以认为是产生球面次波的点波源,而以后任何时刻的波前则可看作是这些次波的包络。
波的反射与折射只能发生在两种介质的交界面上,从反射的原理上区分,可分为吸收反射和直接反射两种类型:吸收反射是指在两种介质的交界面上,介质中具有能与波产生共振的粒子;如果介质中没有能与波产生共振的粒子则称为直接反射。
A. 吸收反射
金属的反光就属于吸收反射,光在以太中传播时,并不产生次波,但当光波遇到金属中的自由电子时,在光波的作用下,自由电子首先吸收光波,从而产生与光波具有相同频率的振动,这时的电子就是点波源,电子振动所产生的波就是次波。在光波与自由电子的作用过程中,入射光被自由电子吸收(共振吸收,这也是金属不透明的原因),反射光是自由电子振动产生的,也就是说,反射光并不是原来的物体发出的,而是金属重新产生的。金属的反光能利用惠更斯原理作出合理的解释,在原理上与相控阵雷达相同。
惠更斯原理的核心是次波,次波又是如何产生的呢?在宏观世界里,我们知道波是由物体振动产生的,当波遇到与介质不同的粒子时,如果这个粒子能在周围介质的作用下产生与波同频率的振动,就可以形成新的波源。但次生光的产生问题又成为关键,如果光是电子跃迁产生的,惠更斯原理是无法应用的。因此,必须假设光是粒子振动产生的、并在以太中传播的波。
产生吸收反射的条件是:粒子必须是自由的,也就是说,粒子吸收能量后没有把能量传给其他的粒子,并且与波源同频振荡。
B. 直接反射
如果介质中不存在能与波产生共振的粒子,波的反射就属于直接反射。在入射介质波阻与折射介质波阻相等的情况下,波不产生反射,也不产生折射。当入射介质波阻与折射介质波阻不相同的情况下,入射端的介质振动能量不可能全部都转化为折射端介质密度的不平衡状态,这必然引起了入射端介质粒子在其运动方向上产生了多余介质粒子的堆积,从而使入射端局部空间产生与振动方向相反的额外密度梯度,使该局部空间的介质粒子产生了与原来振动方向相反振动,这就是反射波波源的起因。在这种情况下,入射波束在界面上的入射点相当于一个波源,因其激发的反射波的介质粒子的振动,恰好与振源介质的振动方向相反,这就是反射波相位与入射波相位反相的原因。在经典物理中,把这种反射波相位与入射波相位相反称之为半波损失,认为波在反射时损失了半个波长,这实际是不正确的,波在反射时并没有发生半个波长的损失,只是反射波是以入射波在入射点为波源而形成的波动,它与入射波已经不是同一列波动,它们当然是反相的。
玻璃的反射属于直接反射。光可以在玻璃中的传播,但玻璃并不是传播介质,可以把玻璃中的原子看成是以太介质中的杂质,由于玻璃中没有自由电子,不存在电子共振吸收,也不存在共振频率与可见光频率相近的原子,同时原子的排列有序,因此,玻璃是透明的。在玻璃的表面,当光波通过时,玻璃内的原子反弹部分以太粒子的波动,这必然引起了入射端以太粒子在其运动方向上产生反向,使部分以太粒子产生了与原来振动方向相反振动,从而产生一定的反射。
虽然光的反射和折射都遵守惠更斯原理,但光的反射与折射具有不同的产生机制,特别是吸收反射,它反射的光是新的波源产生的,但折射的光主要是原来的光。
在两种介质的交界面上,如果存在一种既能吸收光的能量,又不与光波发生共振的粒子,这种介质对入射波是只吸收不反射。具体过程是:光波可以使粒子发生振动,也就是说,粒子可以吸收光能,但粒子吸收光能后,因为粒子并不是独立的,而是与其他的粒子有一定的关联,因此,粒子并不与光波发生共振,从而不反射与入射频率相同的光,但会辐射出比入射光频率低的光,这也是光波能够加热物体的原因。要使光波只吸收不反射,介质需要满足以下要求:
1、介质中粒子可以随着光波振动,便于更好地吸收光的能量;
2、介质中的粒子不能是完全自由的,否则,它将与光波共振;
3、介质最理想的结构为线状结构,便于把振动能量传递给其他的粒子。
对于可见光波,碳纳米管阵列(自由度为2)能满足上述所有要求。
为什么波的反射与折射只发生在两种介质的交界面上?波动在均匀的介质中传播,可以认为这是在两种密度不同的介质中传播的特殊情况,在空间任意找一个平面都可以作为两种介质的分界面。在这种情况下,分界面入射点处的介质粒子的振动速度及相位大小均大小不变、方向不变地从前一种介质密度的介质粒子传递给后一种,而且由于在两种介质中波动的传播速度相等,根据波动属性定律可以判断波动的传播方向并没有发生改变。上一介质粒子的运动动能也完全传递给下一介质粒子,所以,波动在同种均匀的介质中传播不会发生反射。在入射介质密度与折射介质密度相同的情况下,入射端的介质振动动能全部都转化为折射端的介质密度的不平衡状态,所以在入射端并没有多余的介质粒子的累积而使入射端产生与粒子振动方向相反的额外密度梯度,在折射端由入射端介质振动动能产生的介质密度的不平衡引起了介质粒子的属性运动,再以介质粒子的动能形式还原出来,这时粒子动能与上一粒子的动能是完全相同的。
为什么金属网能反射电磁波?在军事上,米波和分米波雷达天线都采用金属网的方式,其效果与金属板是一样的,为什么电磁波没有从缝隙中钻出去呢?这是因为我们所发射的电磁波都是极化的,也就是说,以太介质的运动方式不是简谐振动,而且圆周运动。当电磁波遇到金属网时,在一个周期内总存在碰到自由电子的时候,只要电磁波碰到电子,就能产生吸收反射。
6.5.4. 光速可叠加实验
光速不变而且与参考系无关是相对论中的假设,但至今无人进行实验验证。随着技术的发展,特别是光钟和远程时间校正技术的出现,为实验验证这一假设提供了保障,实验原理如图6-15所示。
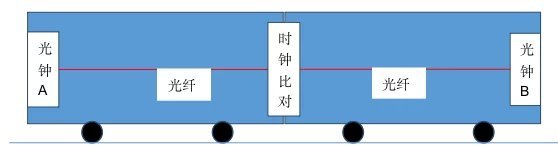
图6-15.光速可变的实验
图中,两个大长方形表示火车车厢,每节的长度为25米,在车厢的两端各放置一套光钟,中间放置一个时钟比对装置,光钟的作用是提供激光同步信号,并通过光纤传到时钟比对装置中,然后比较两个激光信号的时间。
当火车静止时,如果两只光钟已经同步,则时钟比对装置中的输出为0。如何证明光速可以叠加呢?其原理就是火车运动时只能部分拖曳以太,也就是说观察者相对光的传播介质存在运动。由于两个光钟所处的环境相同,而且没有相对运动,可以不考虑相对论效应,因此,只要测出火车在静止与运动这两种状态下,时钟比对装置的输出有无变化,就可以说明光在光纤中的速度是可以叠加。例如:当火车静止时,调整其中的一个光钟,使时钟比对装置的输出为0,如果光速不可叠加,时钟比对装置的输出将与火车的速度无关,如果时钟比对装置的输出与火车的速度相关,则证明光速是可叠加的,如果把光纤放在车厢之外,还可以测量出车厢对以太的拖曳程度。
2022年10月5日,《自然》杂志在线发表了潘建伟团队实现的百公里级的自由空间高精度时间频率传递实验,时间传递稳定度达到飞秒量级,频率传递万秒稳定度优于4×10-19。因此,现代技术已经能够支持上述实验(但本人没有这方面的知识),例如:高铁的速度为80 m/s,由于火车部分拖曳以太,假设光纤内部的以太相对光纤的速度为50 m/s,当光的传播方向与火车的前进方向一致时,光波在光纤中的传播速为V-50 m/s(V是光纤相对以太静止时的传播速度),当光的传播方向与火车的前进方向相反时,光波在光纤中的传播速为V+50 m/s,可以计算出:火车运动时,两只光钟的同步信号到达时钟比对装置的时间差为6.25×10-14 s。如果实验精度不够,可扩展到整列火车(长度400米)。
如果直接通过空气传播光波,火车运动比静止时,两束光的传播时间差别为2.8×10-14 s。
6.6. 光在物体中的传播
由于光的传播介质只有以太,因此,可以把所有物体都看作是杂质,而这些杂质的作用就是吸收光的能量、减小光的速度。
6.6.1. 物体对光的吸收
物体对光的吸收,本质上是将以太的振动能量传给物体的过程,物体对光的吸收主要包括三个部分:一是电子吸收,二是原子吸收,三是分子吸收。
A.电子吸收
电子对光的吸收包括两种:自由电子吸收和束缚电子共振吸收。
对于自由电子,光的吸收主要表现在:光波能够引起自由电子的振动,这也是金属不透明的主要原因。自由电子跟随光波振动的能力与电子的固有频率有关,当光波的频率小于电子的固有频率时,自由电子能够跟随光波的振动,因此,它能够吸收大部分的光波,但当光波的频率大于电子的固有频率时,自由电子跟不上光波的振动,其吸收光波的能力也随着频率的升高而降低(没有明显的吸收峰),这也是入射光的频率增加时,金属的反光特征减弱、X射线能穿透金属的原因。
对于束缚电子,光的吸收存在明显的峰值,其峰值频率在电子的轨道共振频率附近。例如,氢原子基态的半径为53 pm,由于![]() ,可以得出电子的轨道频率为
,可以得出电子的轨道频率为![]() = 6.56×1015 Hz。再如,氧原子外层的基态半径为85 nm,但氧原子外层符合
= 6.56×1015 Hz。再如,氧原子外层的基态半径为85 nm,但氧原子外层符合![]() ,因此,它的外层轨道频率为5.1×1015 Hz,但它的内层电子的轨道频率为
,因此,它的外层轨道频率为5.1×1015 Hz,但它的内层电子的轨道频率为![]() = 3.9×1017 Hz(参见6.4.4)。
= 3.9×1017 Hz(参见6.4.4)。
如果物体中含有氢原子,光波在45.7 nm处就会有一个吸收峰,如果物体中含有氧原子,光波在58.8 nm和0.77 nm处就会有两个吸收峰,如果物体中含有多层电子的原子(钠原子之后),光波会存在多个吸收峰。金属光电效应存在一定的频率范围也是这个原因。
对于激发态的原子,其轨道电子也属于束缚电子,对光同样存在吸收能力,例如,当氢原子处于第一激发态时,就可以吸收波长为121 nm及以下的光,氧原子处于第一激发态时,就可以吸收波长为155 nm及以下的光。需要指出的是,在液体或固体中,一般不存在第二激发态(因为原子间没有第二激发态存在的空间),但第一激发态也是短暂的。
B.原子吸收
原子对光的吸收主要包括两种:原子间伸缩振动和弯曲振动,伸缩振动是指化学键键长的周期变化,而弯曲振动指的是化学键键角的周期变化。
原子对光的吸收与电子吸收的原理相同,都属于振动吸收,是把以太的振动能量转化为原子的振动能量,但吸收的频段不同。例如,二氧化碳分子中,碳原子与氧原子间的伸缩共振频率为7.05×1013 Hz,弯曲共振频率为2×1013 Hz,当光在二氧化碳中传播时,就存在两个主吸收峰,其波长分别是4.26微米和15微米。
如果光的频率小于原子的共振频率,原子能吸收大部分光的能量,但如果光的频率大于原子的共振频率,原子的吸收能力将随着频率的升高而大幅下降。
C.分子吸收
当物体以分子形式存在时,由于分子间的作用力很弱,没有明显的吸收峰,分子对光的吸收与分子的运动状态有关。当分子间以氢键结合时,存在一个较宽的共振吸收态,当分子间以范德瓦尔斯力的形式存在时,没有明显的共振吸收态,但分子的吸收一般只存在于波长大于10微米的远红外区(与分子的质量有关)。
6.6.2. 水对光的吸收
水对光的吸收包括电子吸收、原子吸收和分子吸收,如图6-16所示。

图6-16.水对光波的吸收
电子吸收包括基态吸收和激发态吸收。水中没有自由电子,只有束缚电子。当高频光通过水时,氢原子和氧原子间的共价键会短暂断裂,同时激发电子在高能级轨道上运行,形成激发态吸收。原子吸收包括谐波吸收、伸缩共振吸收、弯曲共振吸收。水分子中氢原子与氧原子间的伸缩共振频率为1.03×1014 Hz(氢原子)和4.89×1013 Hz(氧原子),弯曲共振频率为6.38×1013 Hz(主要是氢原子的振动),当光在水中传播时,存在两个主吸收峰(伸缩振动引起的),其波长分别是2.92微米和6.13微米,其他的吸收峰主要是伸缩振动的谐波,分别是:0.97(3倍)、1.45(2倍)和1.95(3/2倍)微米,另外,还有一个4.7微米弯曲振动的吸收峰。分子吸收包括水分子在氢键的作用下产生的共振吸收,其峰值为17微米,随着波长的增加,水分子对光的吸收能力逐渐减弱。
6.6.3. 玻璃(sio2)对光的吸收
二氧化硅的结构属于晶体,不存在分子吸收,但存在电子吸收和原子吸收。电子吸收包括基态和激发态,原子吸收包括伸缩共振和弯曲共振,但主要是伸缩共振,其中,氧原子的伸缩共振频率为3.29×1013 Hz,弯曲共振频率为2.4×1013 Hz,硅原子的伸缩共振频率为1.4×1013 Hz。当光在二氧化硅中传播时,在红外区存在三个吸收峰,其波长分别是9.1微米、12.5微米和21.4微米。如图6-17所示。
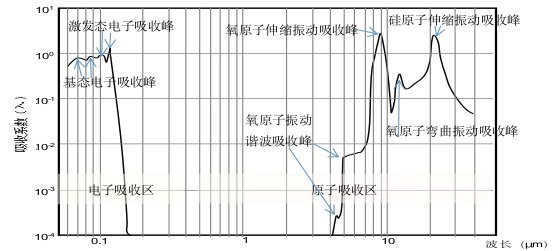
图6-17. 二氧化硅对光波的吸收
6.6.4. 光在物体中的传播速度
光的传播介质是以太,光在普通物体中传播时,除以太粒子外,其他粒子的作用就是降低以太的体积弹性模量。
A.传播速度与物体密度的关系
王祝和先生(大气折射率随高度变化的初步探讨[J].大连海事大学学报, 1984(02):51-57.)已经用实验证明了:当温度不变时,空气的折射率n与压强P的关系为:![]() ,由于压强与密度是线性关系,因此,空气的折射率n与密度ρ的关系也可表示为:
,由于压强与密度是线性关系,因此,空气的折射率n与密度ρ的关系也可表示为:![]() ,其中,当温度为0 0C时,k= 2.26×10-4 m3/kg。邢进华先生(温度对气体折射率的非线性影响[J]. 物理实验, 2005, 25(4):3.)也用实验证明了:当压强不变时,空气的折射率n与温度的关系为:
,其中,当温度为0 0C时,k= 2.26×10-4 m3/kg。邢进华先生(温度对气体折射率的非线性影响[J]. 物理实验, 2005, 25(4):3.)也用实验证明了:当压强不变时,空气的折射率n与温度的关系为:![]() ,其中,α= 0.00366,可以证明:这两个实验完全一致(因为0.00366= 1/273.15,k= 0.000292/1.29)。第二个实验的结果也可表示为
,其中,α= 0.00366,可以证明:这两个实验完全一致(因为0.00366= 1/273.15,k= 0.000292/1.29)。第二个实验的结果也可表示为![]() ,又因为绝对温度
,又因为绝对温度 ,当压强不变时,n-1与大气密度仍然是线性关系,可表示为
,当压强不变时,n-1与大气密度仍然是线性关系,可表示为![]() ,其中p表示压强,R表示气体常数,m表示分子质量。如果把p= 101300帕,R= 8.31,m= 0.029 kg/mol代入,仍然可以得出
,其中p表示压强,R表示气体常数,m表示分子质量。如果把p= 101300帕,R= 8.31,m= 0.029 kg/mol代入,仍然可以得出![]() 。
。
陈伟等人(圆柱微波谐振法测量氩气折射率[J]. 计量学报, 2019(2):7.)以精确的实验也证明了氩气的折射率n与压强P的关系也符合:![]() ,如图6-18所示。
,如图6-18所示。
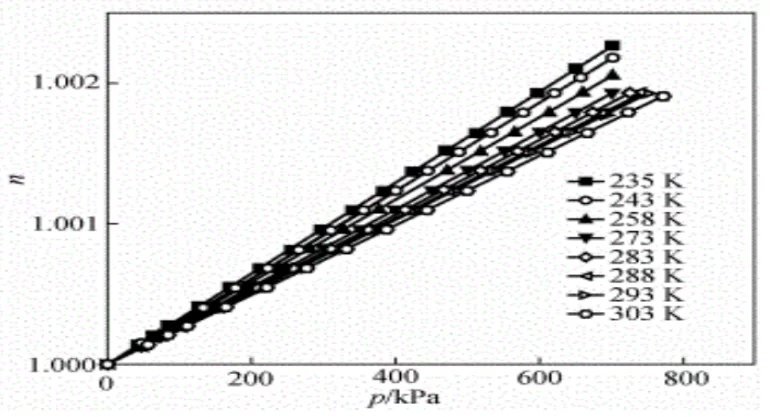
图6-18.氩气的折射率n与压强P的关系
另外,地球大气的密度和折射率随着高度的变化也证明了折射率n与密度ρ的关系也可表示为:![]() ,如表6-5所示。
,如表6-5所示。
表6-5. 地球大气的密度和折射率随着高度的变化

综合多个实验,可以认为:对于任何物体![]() 成立,而且k是一个不随温度变化的常数,光在物体中的传播速度与物体密度的关系可表示为
成立,而且k是一个不随温度变化的常数,光在物体中的传播速度与物体密度的关系可表示为 。
。
B. 传播速度与介电常数的关系
介电常数是电磁场中的物理量,它表示电介质在静电场作用下介电性质或极化性质的参数,根据物质的介电常数可以判别物质的极性大小。通常,相对介电常数大于3.6的物质为极性物质;相对介电常数在2.8~3.6范围内的物质为弱极性物质;相对介电常数小于2.8为非极性物质。例如水的介电常数为81.5,空气的介电常数为1。
传统认为,光的传播速度与介电常数有关:![]() ,实际上,光的传播速度与介电常数没有任何关系,与物质是否是极性物质无关。在电磁波中,ε表示以太的体积压缩系数,与电磁场中的介电常数是两个完全不同的物理量。
,实际上,光的传播速度与介电常数没有任何关系,与物质是否是极性物质无关。在电磁波中,ε表示以太的体积压缩系数,与电磁场中的介电常数是两个完全不同的物理量。
C. 传播速度与光波波长的关系
图6-19和6-20是水和玻璃中,c/v与光波波长的关系图,从图中可以看出:光在物体中传播时,传播速度并不是常数,而是随着波长的变化而变化。
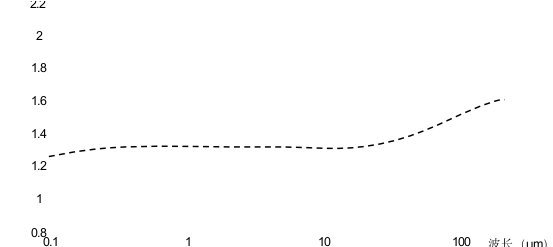
图6-19. 光在水中的速度与波长的关系
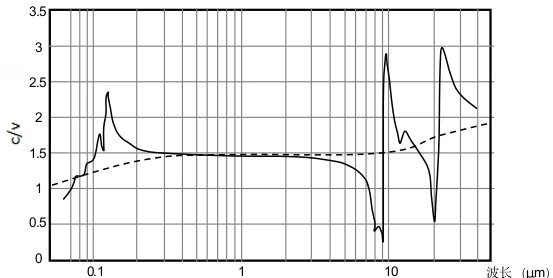
图6-20. 光在玻璃中的速度与波长的关系
是什么原因影响光的速度,特别是在物体的吸收峰处,光的速度会发生剧烈的变化?实质上,光在物体中的速度是不可能变化得如此之大,光的实际速度如图中的虚线所示。
在图中的实线,所表示的是光的相速度(相速度是指电磁波的恒定相位点的速度),并不是光的真实速度。物体对光吸收的原因是光能够引起原子(或电子)的振动,其吸收峰值正是原子(或电子)的共振频率。当光的频率大于共振频率时,由于以太的频率高,因此,以太的振动相位总是比原子的相位变化快,所表现出来的就是光的相速度大,当光的频率小于共振频率时,以太的振动相位总是比原子的相位变化慢,所表现出来的就是光的相速度小。因此,光的折射率是真空中的光速度与介质中的相速度之比(折射率是复数),光的实际速度随着波长增加而减小,其原因是光的能量随着波长增加而减小,当电磁波的频率小于粒子的共振频率时,粒子实际上也参与了波的传播,相当于增加了介质的密度。
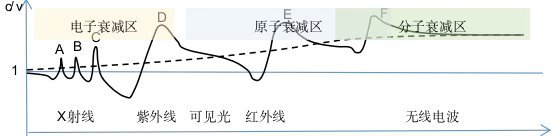
图6-21. 光在物体中传播时的速度与波长的关系
光在物体中的速度可由图6-21描述,其中,实线表示的是相速度,虚线表示实际速度。A、B、C、三个峰值是原子的不同内层电子共振引起的,D是最外层或激态电子共振引起的,E是构成物质较轻原子的伸缩振动引起的,F是较重原子的伸缩振动或分子振动引起的。
6.7. 氢原子的塞曼效应
塞曼效应是物理学史上一个著名的实验,荷兰物理学家塞曼在1896年发现把产生光谱的光源置于足够强的磁场中,磁场作用于发光体,使光谱发生变化,一条谱线即会分裂成几条偏振化的谱线,这种现象称为塞曼效应。
6.7.1. 产生塞曼效应的原因
传统认为:产生塞曼效应的原因是由于原子的磁矩和外磁场相互作用,使原子能级发生分裂。但原子能级的依据是什么?为什么能级会发生分裂?
在量子力学中,氢原子的能级,以量子数表示,氢原子能级从基态开始有:-13.6eV、-3.4eV、-1.51eV、-0.85eV……,但是,这些能级代表什么?为什么具有这些能级?如果这些最基本的内容不讲清楚,是很难让人信服的。
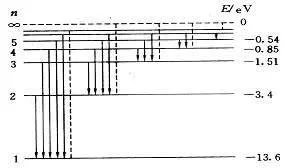
图6-22. 氢原子的能级
本文认为:共振,可以说是一种宇宙间最普遍和最频繁的自然现象之一,氢原子也不例外,它的基态就是共振态,其核外电子的固有频率![]() 与轨道频率
与轨道频率![]() 相等,因此,电子的运动符合
相等,因此,电子的运动符合![]() 。氢原子基态时,电子的轨道参数为:半径 r= 52.9 nm,速度v= 2.188×106 m/s,周期T= 0.152 fs,能量E= -13.6eV,角动量L=
。氢原子基态时,电子的轨道参数为:半径 r= 52.9 nm,速度v= 2.188×106 m/s,周期T= 0.152 fs,能量E= -13.6eV,角动量L=![]() 。
。
当核外电子受到激发时,电子的能量就会升高,处于准共振态(其固有频率为轨道频率的整数倍),对于巴耳末系,电子的固有频率等于2倍的轨道频率,其核外电子的运动符合![]() ,线系限轨道的参数为:半径 r= 211.8 nm,恰好是基态时的4倍,速度v= 1.094×106 m/s,是基态时的2分之一,周期T= 1.22 fs,是基态时的8倍,能量E= -3.4 eV,是基态时的四分之一,角动量L= 2
,线系限轨道的参数为:半径 r= 211.8 nm,恰好是基态时的4倍,速度v= 1.094×106 m/s,是基态时的2分之一,周期T= 1.22 fs,是基态时的8倍,能量E= -3.4 eV,是基态时的四分之一,角动量L= 2![]() ,是基态时的2倍。
,是基态时的2倍。
当氢原子产生Ha线时,电子处于暂稳态(当与线系限轨道的周期比为整数比时,电子在这种轨道中运行的时间比较长),电子的轨道参数为:长半轴 a= 313.4 nm,短半轴 b= 257.6 nm,周期T= 2.19 fs,与线系限轨道的周期比为9:5,能量E= -2.3 eV,角动量L= 2ħ,如图6-23所示。电子与质子间的作用力符合库仑定律和牛顿第二定律,电子的运行轨道符合开普勒三大定律。
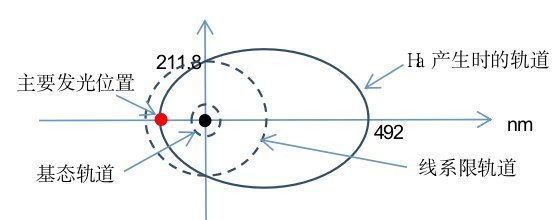
图6-23. 产生Ha时的轨道参数
原子的能级是如何分裂的呢?如图6-24所示,是电子轨道平面与磁场方向不同夹角时的分裂情况。
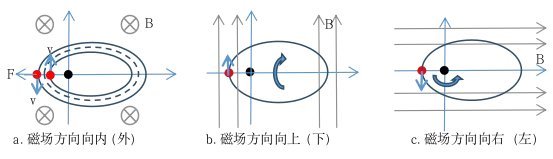
图6-24.磁场的方向与轨道平面的位置
- 当磁场与轨道平面垂直时(图6-24中的a),分为两种情况:一是电子顺时针绕核运行,此时,电子受到向内的洛仑兹力为
 。为了计算简单,电子的轨道可以等效为半径为a(椭圆轨道的半长轴)的园,电子的平均轨道速度为
。为了计算简单,电子的轨道可以等效为半径为a(椭圆轨道的半长轴)的园,电子的平均轨道速度为 = 8.99×105 m/s,电子的轨道角频率为
= 8.99×105 m/s,电子的轨道角频率为 = 2.87×1015 rad/s,当电子在场强为B的磁场中运行时,库仑力与磁场力的和等于向心力:
= 2.87×1015 rad/s,当电子在场强为B的磁场中运行时,库仑力与磁场力的和等于向心力: ,由于磁场力很小(与库仑力不在一个数量级),电子的速度和半径的改变量也很小,设速度的改变量为∆v,可以认为电子所受的磁场力与增加的离心力相等::
,由于磁场力很小(与库仑力不在一个数量级),电子的速度和半径的改变量也很小,设速度的改变量为∆v,可以认为电子所受的磁场力与增加的离心力相等:: ,忽略小项,可得角速度的变化量:
,忽略小项,可得角速度的变化量: 。也就是说,电子的轨道频率f增加了
。也就是说,电子的轨道频率f增加了 (一个洛仑兹单位)。
(一个洛仑兹单位)。
二是电子逆时针绕核运行,同理可以算出电子的轨道角频率的减小量为 。
。
从上面的过程描述可以看出:原子能级的分裂是由于电子受到洛仑兹力的作用所导致的,轨道角频率的改变量为 ,其中θ是电子的轨道平面与磁场方向的夹角,当θ= 0时,原子能级不发生分裂。
,其中θ是电子的轨道平面与磁场方向的夹角,当θ= 0时,原子能级不发生分裂。
6.7.2. 原子的发光过程
原子发光时,主要的发光区在近核点(此处的急动度最大),发光的方向与电子运动的方向一致,如图6-25a所示。
单个原子的发光具有单向性,它的投影是一条线,在近核点的强度最大,其他点的光强分布与高斯分布类似。

图6-25. 原子发光的过程
6.7.3. 偏振光的产生
光之所以偏振是与光的产生过程分不开的,如果电子是直线简谐振动,所产生的光就是纵波,正是因为电子的曲线运动,所产生的光才是偏振的。
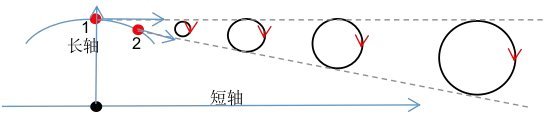
图6-26. 偏振光的产生过程
如图6-26所示,电子的运动可以引起以太的振动,与空气中声音产生的过程类似。由于波在以太中的传播速度是光速,而电子的运动速度小于光速,因此,当电子运行到图中1的位置时所发出的波,总是比电子运行到图中2的位置时所发出的波的相位超前。在波的传播过程中,由于波的叠加,导致了介质的振动不是直线简谐振动,而是圆周运动。这种介质粒子为圆周运动的波就是偏振波,而且是线偏振波(波源与介质的振动在同一个平面内)。
光的偏振是光源产生的,与传播过程无关,光向什么方向偏振主要是看粒子发光的同时,光源的运动轨迹,如果光源发光的同时,其运动轨迹在同一个平面内,它发出的光就是线偏振,而且光的偏振方向一定与电子轨道所在的平面平行,并且与光的传播方向垂直;如果光源在发光的同时,其运动轨迹不在同一个平面内,它发出的光就是圆偏振或椭圆偏振。
6.7.4. 对原子发光的观察
用望远镜观察氢灯时,所看到的氢原子所发出的光,其电子轨道的短轴必须平行于观察者的方向,而且电子在近核点的运动方向也必须朝着观察者(否则,观察者看不到),但轨道长轴可以是任意角度。
A. 垂直于磁场方向观察时
当观察者垂直于磁场方向时,所观察到的光只能是图8-4中a和c两种情况。在a中,只有角频率为 (称为σ+)和
(称为σ+)和 (称为σ-)的光,没有角频率为
(称为σ-)的光,没有角频率为![]() 的光,但在c中,只有角频率为
的光,但在c中,只有角频率为![]() 的光(称为π光),而没有其他。为什么c 中存在轨道平面旋转,而没有产生其他频率的光呢?这是因为电子轨道平面是绕焦半径旋转的,发光的方向并没有改变(一直平行于短轴),而且发光点的旋转半径为135 nm,仪器是无法分辨的。
的光(称为π光),而没有其他。为什么c 中存在轨道平面旋转,而没有产生其他频率的光呢?这是因为电子轨道平面是绕焦半径旋转的,发光的方向并没有改变(一直平行于短轴),而且发光点的旋转半径为135 nm,仪器是无法分辨的。
为什么π光的偏振方向平行于磁场方向,而σ光却垂直于磁场方向?
π光是图8-3c中的状态下产生的,此时,轨道的长轴与磁场的方向平行,因而,π光的偏振方向平行于磁场方向。
σ光是图8-3a中的状态下产生的,此时,轨道平面与磁场的方向垂直,因而,σ光的偏振方向垂直于磁场方向。
B. 顺着磁场方向观察时
当顺着磁场方向观察时,所观察到的光是图6-24 b中的状态下产生的,从图中可以看到,电子的轨道能级并没有分裂,但为什么观察到的是两个分裂的光谱呢?
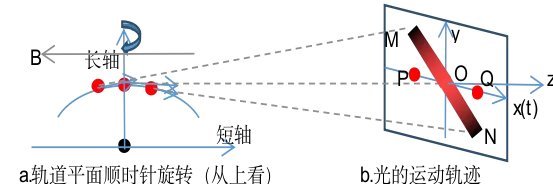
图6-27.光谱分裂的原因
由于磁场方向平行于短轴,在磁场力的作用下,原子(指能看到发光的原子)核外电子的轨道周期不变,但由于电子轨道绕长轴旋转,也就是说,电子所发出的光的方向也会改变,因此,观察者所看到的光实际上是一种调制光。由于电子绕核运行的角频率为![]() ,轨道平面旋转的角速度为
,轨道平面旋转的角速度为![]() ,观察者所看到的光可用
,观察者所看到的光可用![]() 表示,根据三角函数公式,可写
表示,根据三角函数公式,可写![]() ,如图6-27所示。当光的轨迹从M点运动到O点时,所观察到的光是
,如图6-27所示。当光的轨迹从M点运动到O点时,所观察到的光是![]() ,而从O点运动到N点时,所观察到的光是
,而从O点运动到N点时,所观察到的光是
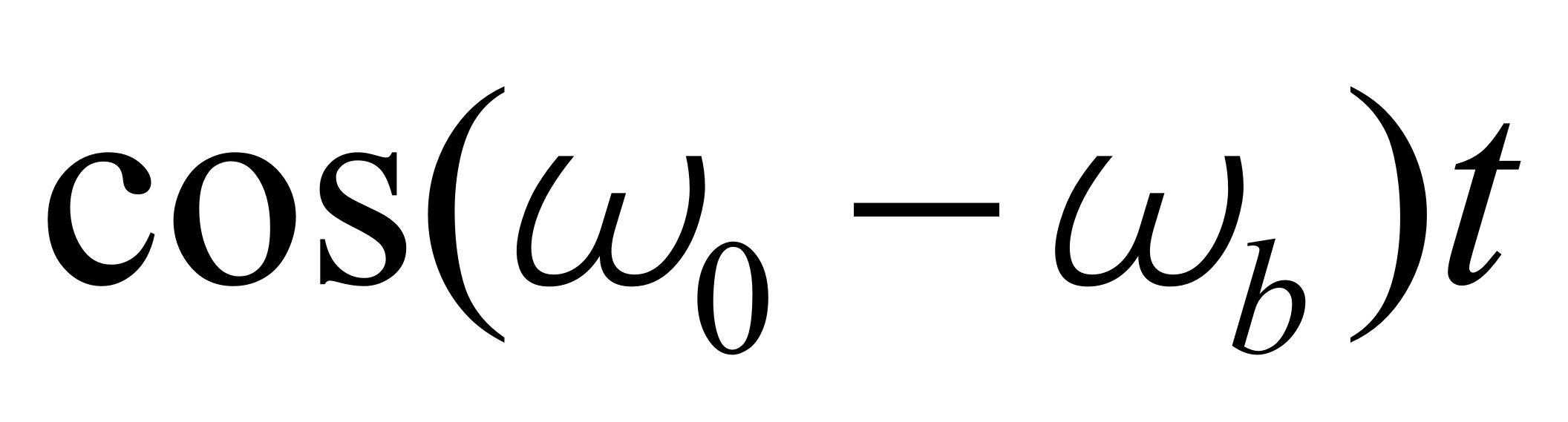 。在通信理论中称为无载波调制,这就是只能观察到两个边带信号而没有载波的原因。需要指出的是:
。在通信理论中称为无载波调制,这就是只能观察到两个边带信号而没有载波的原因。需要指出的是: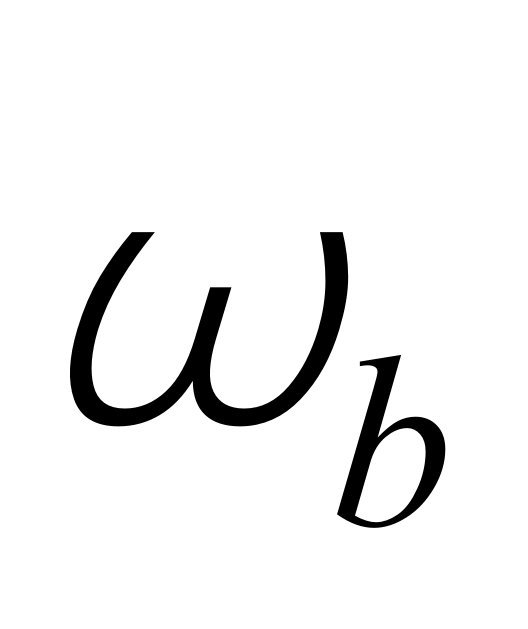 与
与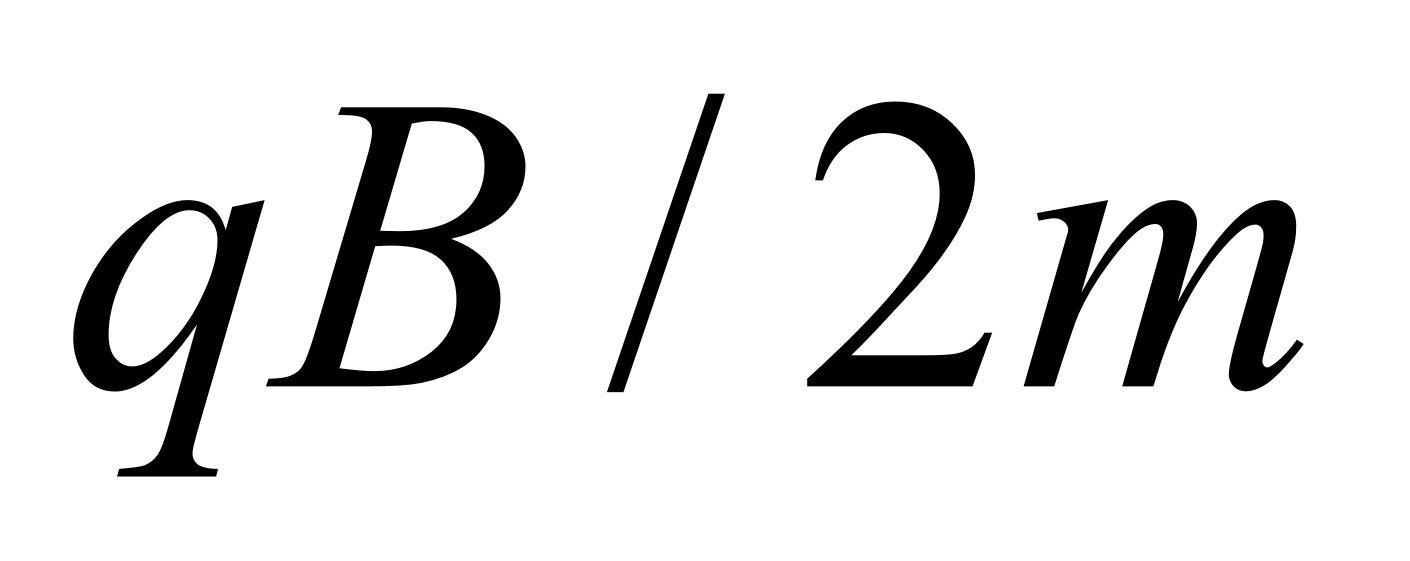 不一定相等。
不一定相等。可以看出:原子发出的光并没有分裂,光谱分裂的原因是观察效应(类似于多普勒效应),发光方向的转动实际上是对光的相位调制。
电子在近核点附近的运动,包括三个方向,如图6-27所示:一是向右运动,这个速度很大,其作用就是引起以太的振动(也就是产生光);二是上下运动,这椭圆运动的特点,正是由于电子运动速度方向的改变,才导致了轨道平面内线偏振的产生;三是前后运动,电子在近核点上并不受磁场的影响,是电子的惯性运动,是由于轨道平面绕长轴旋转,才使电子运动速度方向发生改变,从而也导致与轨道平面垂直方向上线偏振的产生。两个相互垂直的线偏振在空间叠加,就是圆偏振。
圆偏振光只是对两个正交的线偏振光叠加后的一种描述,光并不是真的按照圆的轨迹运动,而是一条直线,如图8-6所示。两个幅度相同的两个正交线偏振光叠加后就是圆偏振光,但这两束光是各自独立地传播。例如,光通过1/4波片时,根据波片的快轴,分解为两束光,分为平行于快轴和垂直快轴的正交偏振光,分别沿着不同的路径传播,如图6-28所示。

图6-28. 圆偏振的本质
当线偏振光垂直于波片平面入射时,平行于快轴与垂直于快轴的光沿着同一条路径,混合后的光,我们称为圆偏振,但这两种光事实上是相对独立的,并不存在圆形偏振,如果再次通过一个1/4波片,它又是一个线偏振,而且这个波片的快轴即可以与上面的波片快轴平行,也可以垂直。
圆偏振光的方向是如何判断的呢?是以波片的快轴为标准的,当快轴的方向![]() 、入射光的线偏振方向
、入射光的线偏振方向![]() 和光的传播方向
和光的传播方向![]() 符合右手定则
符合右手定则![]() 时,我们称出射光为左旋圆偏振光,否则为右旋圆偏振光。
时,我们称出射光为左旋圆偏振光,否则为右旋圆偏振光。
光并不旋转(声波也没有旋转特征),只是为了区分圆偏振的方向而人为规定的。如图8-6所示,当光的轨迹从M点运动到O点时,所观察到的光的频率比实际的频率高,因为光是向着观察者移动;而从O点运动到N点时,所观察到的光的频率比实际的频率低,因为光是远离观察者。
如果以光的传播方向为z轴,以时间为x轴建立坐标系,它与电子的轨道平面垂直,y轴代表与中心的偏移量,其方向符合![]() ,如图8-7所示。
,如图8-7所示。
圆偏振属于观察效应。由于频率的分裂,要想判断圆偏振的方向,必须把观察点在时间轴上前推或后移。也就是说,判断MO这段光的偏振方向,观察点应后移,放在图中P的位置;判断ON这段光的偏振方向,观察点应前推,放在图中Q的位置。
圆偏振的判断规则是:伸出右手,拇指指向光的传播方向,四指指向光的轨迹运动方向,如果观察点在手心方向,定义为右旋,否则为左旋。
C. 逆着磁场方向观察时
如图6-29所示,电子在近核点的运动方向与磁场方向一致,与顺着磁场观察唯一不同的就是圆偏振的旋转方向。当逆着磁场方向观察时,根据定义,高频光为左旋,低频光为右旋。
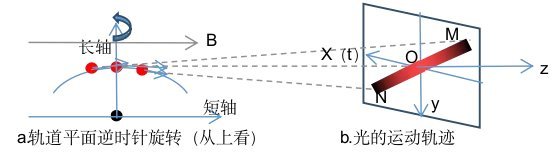
图6-29.圆偏振方向的区别
6.7.5. 光致旋转效应
光致旋转效应本来与塞曼效应没有关系,但量子力学认为:光子具有自旋角动量,光子的自旋决定了光的偏振。1936年,美国普林斯顿大学的Beth根据四分之一波片可改变圆偏振旋向的性质,利用力学实验巧妙地验证了左、右圆偏振光分别具有自旋角动量![]() ,如图6-30所示。
,如图6-30所示。
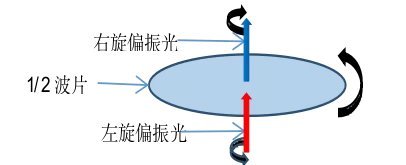
图6-30.证明光具有角动量的实验
当左旋偏振光通过1/2波片后,变为右旋偏振光,同时,1/2波片也逆时针旋转(从上看),说明了光具有角动量。
光是波,怎么可能具有角动量呢?如果光没有角动量,上述实验如何解释?
光可以使物体旋转已经被实验证实,但是,是什么力推动的?到目前为止,我们并不知道光子是什么,也不知道它为什么转动。是电磁力推动波片旋转吗?显然不是,因为波片是中性的。
Beth的实验并不能证明光子具有自旋角动量,因为只有双折射晶体才能有此效应,属于孤证。如果光子确实具有角动量,其他物体也应该能发生旋转。
如果光子没有角动量,是什么推动波片旋转的呢?本文认为是光压。因为双折射晶体的晶胞面并不与晶体的表面平行或垂直,当光垂直入射晶体表面时,非常光所产生的光压会与晶体表面形成一成的角度,正是光压所产生的分力推动了波片的旋转。
另外,用电磁理论对波片的解释还存在一个缺陷:当线偏振光通过1/2波片时,寻常光(o光)与非常光(e光)的相位相差应为180度(或它的整数倍),这两束光叠加后,按道理应该相互削弱,但实际情况并不是。
6.7.6. 反常塞曼效应
反常塞曼效应是由于原子的内层电子在外磁场的作用下出现的轨道变化,进而影响到外层电子轨道变化所表现出来的一种现象。
由于氢原子没有内层电子,所以氢原子不存在反常塞曼效应。
6.7.7. 小结
塞曼效应与电磁理论无关,更不能证明空间取向量子化。量子理论只有众多的假设和数学的推导,没有物理过程。例如,量子理论中不承认电子具有轨道,但却承认原子具有精确的能级和固定的角动量,也不说明能级和角动量是从哪里来的;认为光是电子跃迁产生的,但却无法说明跃迁的过程和光子的前进方向;提出选择定则,却无法说明理由;认为光的偏振来源于光子的自旋,却不知道光子是什么。
塞曼效应可以说明:
- 原子发光是电子椭圆运动产生的,电子在近核点的发光最强,发光的方向为电子运动的切线方向;
- 原子谱线的分裂是洛仑兹力作用的结果;
- 光的偏振与光源有关,与传播过程无关。
6.8. 以太与名人录
古希腊人认为:时间与空间不是这个世界的真理,没有以太,一切将不复存在,任何事物都将失去意义,以太本身才是真理。
特斯拉说:“不认识到以太的存在,以及它在现象世界里发挥的不可缺少作用,所有对宇宙运作的尝试解释都是无用的”。
汤姆逊在1909年宣称:“以太并不是思辩哲学家异想天开的创造,对我们来说,就象我们呼吸空气一样不可缺少”。
洛伦兹认为以太是一种很特别的物质:以太没有质量,绝对静止,不与任何物质反应,仅仅是电磁运动的荷载物。
以太的否定与迈克尔逊的实验有关,但迈克尔逊本人却相信以太的存在,至死还念念不忘“可爱的以太”。
1920年,爱因斯坦说:“根据广义相对论,空间是具有物理性质的,没有以太的空间是无法想象的,但根据狭义相对论,只是不需要以太,并不是全盘的否认!”
1970年狄拉克指出:“以太观念并没有死掉,只要基本问题仍未得到解决,必须记住这里还有一种可能性。”
美籍物理学家张操说:“现代物理学一方面否定以太的存在,另一方面却引入了物理真空的概念。其实,‘物理真空’仅是以太的一个代名词”。
……
以太被否定已有一个多世纪了,但复出呼声始终不绝。
本文认为:以太与空气具有高度相似的性质,在地球上,以太只有一个作用:电磁波的荷载物,不存在以太绝对参考系,以太也不参与电磁作用。

 ,由于磁场力很小(与库仑力不在一个数量级),电子的速度和半径的改变量也很小,设速度的改变量为∆v,可以认为电子所受的磁场力与增加的离心力相等::
,由于磁场力很小(与库仑力不在一个数量级),电子的速度和半径的改变量也很小,设速度的改变量为∆v,可以认为电子所受的磁场力与增加的离心力相等:: ,忽略小项,可得角速度的变化量:
,忽略小项,可得角速度的变化量: 。也就是说,电子的轨道频率f增加了
。也就是说,电子的轨道频率f增加了

无数事实说明;只有把全副身心投入进去;专心致志;精益求精;不畏劳苦;百折不回;才有可能攀登科学高峰。
独立思考能力;对于从事科学研究或其他任何工作;都是十分必要的。在历史上;任何科学上的重大发明创造;都是由于发明者充分发挥了这种独创精神。
科学的探讨与研究;其本身就含有至美;其本身给人的愉快就是报酬;所以我在我的工作里面寻得了快乐。
一个人在科学探索的道路上走过弯路犯过错误并不是坏事;更不是什么耻辱;要在实践中勇于承认和改正错误。
科学的惟一目的是减轻人类生存的苦难;科学家应为大多数人着想。
青年的敏感和独创精神;一经与成熟科学家丰富的知识和经验相结合;就能相得益彰。
社会一旦有技术上的需要;则这种需要就会比十所大学更能把科学推向前进。
在科学思维中常常伴着诗的因素;真正的科学和真正的音乐要求同样的想象过程。
在新的科学宫里;胜利属于新型的勇敢的人;他们有大胆的科学幻想;心里燃烧着探求新事物的热情。
智慧不属于恶毒的心灵;没有良心的科学只是灵魂的毁灭。
在科学上最好的助手是自己的头脑;而不是别的东西。
在科学工作中;不愿意越过事实前进一步的人;很少能理解事实。
科学是老老实实的东西;它要靠许许多多人民的劳动和智慧积累起来。
科学决不是也永远不会是一本写完了的书。每一项重大成就都会带来新的问题。任何一个发展随着时间的推移都会出现新的严重的困难。
如果学习只在于模仿;那么我们就不会有科学;也不会有技术。